1.3.3.3. Неплоская четырехузловая DKT - оболочка
Рассмотрим DKT -
элемент тонкой неплоской четырехузловой оболочки с прямыми ребрами. Этот
элемент не имеет локальной системы координат, как плоские двумерные элементы, а
описывается в глобальной системе координат ![]() (рис. 1.3.3.5).
(рис. 1.3.3.5).
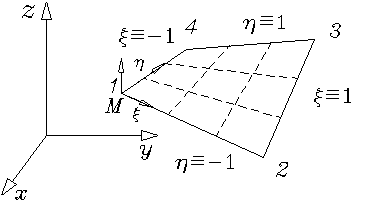
Рис. 1.3.3.5
Тип элемента в [ИСПА] - 314. Угол неплоскостности ![]() элемента меняется в
пределах:
элемента меняется в
пределах: ![]() .
.
Геометрия элемента задается параметрическими формулами:
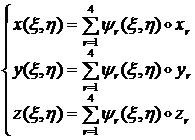 (1.3.3.3.1)
(1.3.3.3.1)
где ![]() - координаты узлов при
вершинах элемента;
- координаты узлов при
вершинах элемента;
![]() - билинейные функции формы
- билинейные функции формы
определенные на
квадрате (2x2) в плоскости ![]() (см. рис.1.3.3.6).
(см. рис.1.3.3.6).
Билинейные функции
формы были определены в п.1.3.1.3.
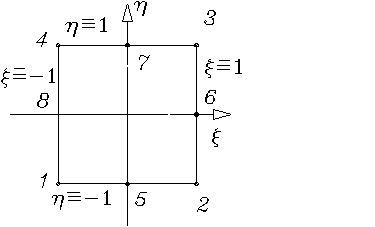
Рис. 1.3.3.6
В каждом узле ![]() элемента по 6 степеней
свободы:
элемента по 6 степеней
свободы:
три компоненты вектора
перемещения узла 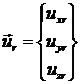 , и три компоненты вектора углов поворота
, и три компоненты вектора углов поворота 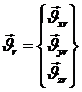 вектора нормали
вектора нормали ![]() вокруг осей
вокруг осей
![]() .
.
Вектор степеней
свободы узла ![]() равен:
равен: 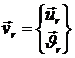
Будем также
рассматривать вектор степеней свободы узла 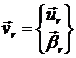
где 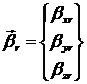 - вектор
углов поворота вектора нормали в
узле к осям
- вектор
углов поворота вектора нормали в
узле к осям ![]() .
.
Вектор степеней
свободы элемента ![]() . Всего у элемента 6x4=24 степеней свободы.
Поэтому вектор степеней свободы элемента
. Всего у элемента 6x4=24 степеней свободы.
Поэтому вектор степеней свободы элемента ![]() имеет 24
компоненты.
имеет 24
компоненты.
В п. 1.3.3.1. мы
установили вид поля вектора перемещений точек оболочки:
![]() (1.3.3.3.2)
(1.3.3.3.2)
По аналогии с
п.1.3.1.3 для четырехузлового элемента мембраны, поле вектора мембранных
перемещений ![]() аппроксимируется с помощью билинейных функций
формы
аппроксимируется с помощью билинейных функций
формы ![]() , использованных для аппроксимации геометрии
элемента (формула 1.3.3.3.1):
, использованных для аппроксимации геометрии
элемента (формула 1.3.3.3.1):
![]() (1.3.3.3.3)
(1.3.3.3.3)
По аналогии с п.
1.3.2.4 для четырехузлового DKT -
элемента тонкой пластины введем дополнительные срединные узлы ![]() , расположенные по середине соответствующих
ребер элемента
оболочки (рис. 1.3.3.7).
, расположенные по середине соответствующих
ребер элемента
оболочки (рис. 1.3.3.7).
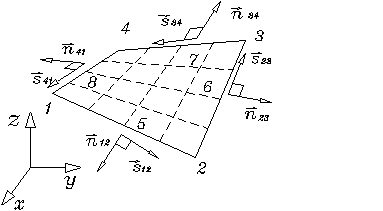
Рис.
1.3.3.7
![]()
Введем в каждом
срединном узле по три зависимые степени свободы:
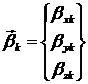
Тогда, как и в
п.1.3.2.4, для описания компонент векторной функции ![]() имеем по
8 степеней свободы
имеем по
8 степеней свободы ![]() .
.
Поэтому ![]() можно
аппроксимировать с помощью биквадратичных функций формы
можно
аппроксимировать с помощью биквадратичных функций формы ![]() :
:
![]() (1.3.3.3.4)
(1.3.3.3.4)
Положение срединных
узлов на квадрате в плоскости ![]() показано
на рис. 1.3.3.6.
показано
на рис. 1.3.3.6.
Формулу (1.3.3.3.4) надо видоизменить, исключив
из нее введенные зависимые степени свободы. Кроме того, необходимо выбрать
такую аппроксимацию ![]() , чтобы выполнялись условия Кирхгоффа.
, чтобы выполнялись условия Кирхгоффа.
Как и в п. 1.3.2.4,
потребуем выполнения следующих условий:
1) выполнения условий
Кирхгоффа (1.3.3.1.18) в вершинных узлах:
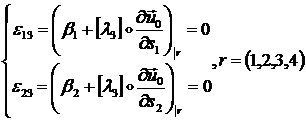 (1.3.3.3.5)
(1.3.3.3.5)
2) выполнения условий
Кирхгоффа для сдвиговой деформации вдоль
сторон четырехугольного элемента в его срединных узлах:
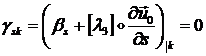 (1.3.3.3.6)
(1.3.3.3.6)
3) линейный закон
изменения вдоль ребра ![]() угла
поворота
угла
поворота ![]() вектора
нормали
вектора
нормали ![]() к
векторам
к
векторам ![]() , перпендикулярным к ребрам и вектору нормали
, перпендикулярным к ребрам и вектору нормали ![]() в данной
точке ребра:
в данной
точке ребра:
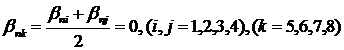 (1.3.3.3.7)
(1.3.3.3.7)
4) кубический закон
изменения вдоль ребра ![]() перемещения
перемещения ![]() ; из него следует:
; из него следует:
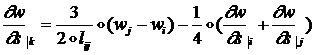 (1.3.3.3.8)
(1.3.3.3.8)
Заметим, что для
неплоского четырехугольника остаются постоянными вдоль данного ребра ![]() только
вектора
только
вектора ![]() , тогда как вектора нормали к поверхности
, тогда как вектора нормали к поверхности ![]() и вектора
и вектора
![]() меняются
вдоль ребра
меняются
вдоль ребра ![]() . В частности, из этого следует, что условие
(1.3.3.3.6) для
. В частности, из этого следует, что условие
(1.3.3.3.6) для ![]() вместе с
другими условиями не обеспечивают выполнения условий Кирхгоффа вдоль контура элемента.
вместе с
другими условиями не обеспечивают выполнения условий Кирхгоффа вдоль контура элемента.
Поэтому потребуем, чтобы угол неплоскостности ![]() был
достаточно малым (угол
был
достаточно малым (угол ![]() можно определить,
например, как максимальный
по величине угол между векторами нормали
можно определить,
например, как максимальный
по величине угол между векторами нормали ![]() в
вершинных углах элемента).
в
вершинных углах элемента).
Поэтому в дальнейшем
будем считать:
![]() (1.3.3.3.9)
(1.3.3.3.9)
Тогда условия
(1.3.3.3.6) принимают обычный вид:
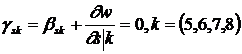
Теперь можно считать
условия Кирхгоффа справедливыми
вдоль контура неплоской оболочки:
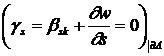
Как и в п. 1.3.2.4,
это приводит для малого элемента к выполнению условий Кирхгоффа для всей поверхности,
т.е. мы получили элемент тонкой неплоской оболочки.
Преобразуем теперь
формулу (1.3.3.3.4) аппроксимации ![]() с помощью
(1.3.3.3.5) - (1.3.3.3.9):
с помощью
(1.3.3.3.5) - (1.3.3.3.9):
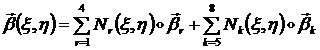 (1.3.3.3.10)
(1.3.3.3.10)
где разложим ![]() по ортогональному
реперу
по ортогональному
реперу ![]()
![]()
Если потребовать,
чтобы вдоль каждого ребра ![]() проекция
проекция ![]() велась на репер
велась на репер ![]() в срединном узле (т.е.
здесь учтено допущение (1.3.3.3.9):
в срединном узле (т.е.
здесь учтено допущение (1.3.3.3.9): ![]() ), то с помощью указанных формул закон аппроксимации
), то с помощью указанных формул закон аппроксимации ![]() может быть выражен
следующим образом:
может быть выражен
следующим образом:
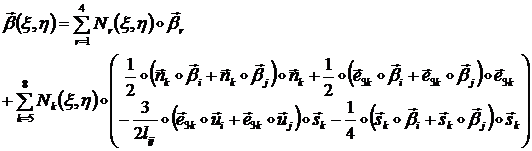
(1.3.3.3.11)
где ![]() - вершинные узлы,
относящиеся к ребрам со срединным узлом;
- вершинные узлы,
относящиеся к ребрам со срединным узлом;
![]()
Видим, что здесь ![]() аппроксимирован только
через независимые степени свободы
аппроксимирован только
через независимые степени свободы ![]() .
.
Рассмотрим следующую
проблему. Пусть вектор степеней свободы элемента
![]() , где
, где ![]() - такой, что значения
его компонент определяются параллельным
переносом
- такой, что значения
его компонент определяются параллельным
переносом ![]() и поворотом
и поворотом ![]() системы узлов элемента
как целого:
системы узлов элемента
как целого:
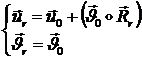
где: ![]() - радиус-вектор узла
- радиус-вектор узла ![]() . Тогда при правильной аппроксимации перемещений
. Тогда при правильной аппроксимации перемещений ![]() и углов
и углов ![]() они должны
удовлетворить условию параллельного переноса
они должны
удовлетворить условию параллельного переноса ![]() и поворота
и поворота ![]() элемента как целого:
элемента как целого:
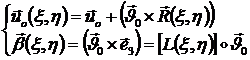 (1.3.3.3.12)
(1.3.3.3.12)
Из формулы (1.3.3.3.3)
аппроксимации ![]() следует:
следует:
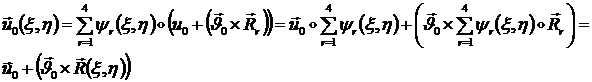 т.е. поле
т.е. поле ![]() отвечает указанному
требованию. Здесь мы воспользовались свойством
отвечает указанному
требованию. Здесь мы воспользовались свойством ![]() :
: ![]()
Но
для ![]() , определяемого формулой (1.3.3.3.11), это требование не
будет выполняться. Это приведет к появлению ложных деформаций элемента. Поэтому,
учитывая условие
, определяемого формулой (1.3.3.3.11), это требование не
будет выполняться. Это приведет к появлению ложных деформаций элемента. Поэтому,
учитывая условие ![]() , изменим формулу (1.3.3.3.11) таким образом, чтобы условие
(1.3.3.3.12) для
, изменим формулу (1.3.3.3.11) таким образом, чтобы условие
(1.3.3.3.12) для ![]() :
: ![]() выполнялось бы тождественно.
Это можно сделать, заменив матрицы
выполнялось бы тождественно.
Это можно сделать, заменив матрицы ![]() в узлах
в узлах ![]() на их значение в
точке интегрирования
на их значение в
точке интегрирования ![]() .
.
Окончательная формула
следующая (1.3.3.3.13):
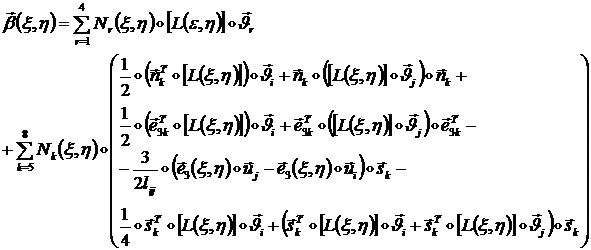
Введя вектора степеней
свободы узлов 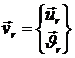 , формулу (1.3.3.3.13) можно представить в виде:
, формулу (1.3.3.3.13) можно представить в виде:
![]() (1.3.3.3.14)
(1.3.3.3.14)
где: ![]() - матрица функций
формы для
- матрица функций
формы для ![]() .
.
Подставив в формулы
(1.3.3.1.27) для ![]() формулу (1.3.3.3.3)
для аппроксимации
формулу (1.3.3.3.3)
для аппроксимации ![]() и формулу
(1.3.3.3.14) для аппроксимации
и формулу
(1.3.3.3.14) для аппроксимации ![]() , получим аппроксимационные формулы для
, получим аппроксимационные формулы для ![]() :
:
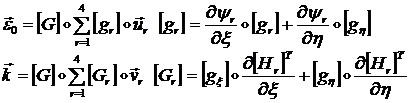
(1.3.3.3.15)
Введем матрицы:
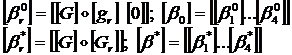
Тогда формулы
(1.3.3.3.15) примут вид:
![]() (1.3.3.3.16)
(1.3.3.3.16)
где естественно
назвать:
![]() - мембранная матрица
деформирования;
- мембранная матрица
деформирования;
![]() - изгибная матрица
деформирования.
- изгибная матрица
деформирования.
Тогда энергии
деформаций ![]() и
и ![]() из (1.3.3.1.34)
примут вид:
из (1.3.3.1.34)
примут вид:
![]() (1.3.3.3.17)
(1.3.3.3.17)
где введены мембранная
![]() и изгибная
и изгибная ![]() матрицы жесткости:
матрицы жесткости:
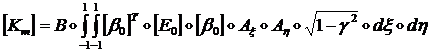
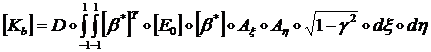
(1.3.3.3.18)
Интегрирование ведется
по квадрату (2x2) в плоскости ![]() (рис. 1.3.3.6).
Численное интегрирование по Гауссу матрицы
(рис. 1.3.3.6).
Численное интегрирование по Гауссу матрицы ![]() можно вести с порядком
(2x2), а матрицы
можно вести с порядком
(2x2), а матрицы ![]() - (3x3).
- (3x3).
Таким образом, мы
нашли матрицу жесткости оболочки:
![]()
Численные тесты
данного элемента показывают, что он
удовлетворительно работает при значениях угла неплоскостности ![]() в интервале:
в интервале:
![]()