1.3.3 Элементы оболочки
1.3.3.1 Понятие оболочки. Теория тонкой оболочки
ОПРЕДЕЛЕНИЕ
Оболочкой будем называть двумерный элемент с произвольной
геометрией его поверхности, который в
общем случае может воспринимать действие 6-и силовых факторов: вектора сил 
и вектора моментов сил
.
Здесь введена глобальная
система координат 
(г.с.к.), в которой
описывается произвольная оболочка. Рассмотрим теорию тонкой оболочки, толщина 
которой много меньше
характерного размера оболочки в двух других направлениях [6,8]. На рис.
1.3.3.1 изображена оболочка в системе координат .
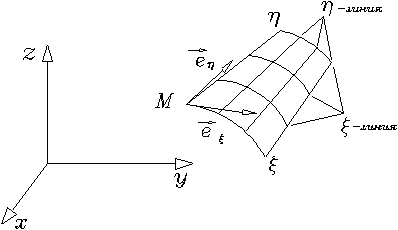
Рис. 1.3.3.1
Рассмотрим
сначала вопрос описания геометрии произвольной тонкой недеформированной
оболочки [6]. Как и в п. 1.3.2.1, где рассматривалась теория тонкой пластины,
введем понятие нейтральной поверхности. Нейтральная поверхность характеризуется
тем, что она равноудалена от "верхней" и "нижней"
поверхностей оболочки и на ней отсутствуют изгибные деформации (хотя мембранные
деформации, конечно, в общем случае есть). Поэтому для описания геометрии
оболочки достаточно описать нейтральную поверхность.
Так
как положение произвольной точки 
поверхности
можно задать с помощью двух параметров, то мы будем считать заданным
параметрический закон описания геометрии нейтральной поверхности:
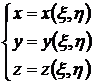(1.3.3.1.1)
Будем
называть 
- линией
кривую на нейтральной поверхности с постоянным значением параметра 
, а - линией
- кривую с постоянным значением . Два семейства кривых образуют на поверхности
координатную сетку (рис. 1.3.3.1). Поэтому параметры 
можно назвать
криволинейными координатами поверхности.
Бесконечно
малый отрезок -
линии, который обозначим через 
, связан с дифференциалом 
соотношением:
(1.3.3.1.2)
где: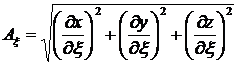 
Аналогично определяется
дифференциал 
:
(1.3.3.1.3)
где: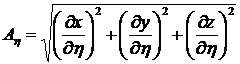 
Рассмотрим
далее на поверхности произвольную точку и введем
единичный вектор 
, касательный к - линии в
этой точке. Его компоненты в г.с.к. представим матрицей:
(1.3.3.1.4)
где: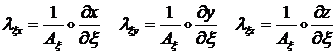 
Заметим,
что: 
как
и должно быть для суммы квадратов компонент единичного вектора.
Аналогично
введем единичный вектор 
, касательный к - линии в
т. . Его компоненты представим матрицей:
(1.3.3.1.5)
где: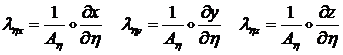 
При этом: 
Скалярное произведение
будем
обозначать через 
;
в матричном представлении: 
(1.3.3.1.6)
Из
рисунка 1.3.3.1 ясно, что: 
, где: 
- угол
между и . В случае ортогональности и - линий в
т. : 
.
Построим
теперь в произвольной точке поверхности
локальный ортогональный репер 
:
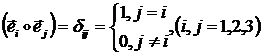
Для
каждого единичного вектора 
построим
матрицу его компонент в г.с.к. : 
Выберем 
, тогда:
(1.3.3.1.7)
Вектор
перпендикулярен к 
и лежит в
плоскости, касательной к поверхности оболочки в т. М. Если потребовать, чтобы 
, то вектор определится
однозначно:
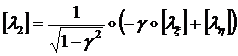(1.3.3.1.8)
Дифференциалы:
(1.3.3.1.9)
Чтобы
репер образовал
правую систему координат, потребуем, чтобы 
был равен
векторному произведению: 
откуда
следует что:
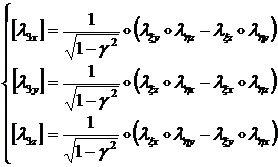(1.3.3.1.10)
Ясно, что вектор является нормальным
к поверхности оболочки в т. : 
.
Перейдем
теперь к вопросу о деформации произвольной тонкой оболочки. Пусть в результате
деформации оболочки точки нейтральной поверхности получили перемещения, описывающиеся
полем вектора 
. Все перемещения точек оболочки 
будем
считать малыми 
. В произвольной точке нейтральной поверхности единичный вектор задает
ось 
, нормальную к поверхности в этой точке. В
пределах оболочки меняется
в пределах: 
Так
как перемещения точек оболочки малы по сравнению с толщиной оболочки , то как и
в п. 1.3.2.1 при рассмотрении теории тонкой пластины, мы можем разложить поле
вектора перемещений 
в
произвольной точке 
(удаленной от т. по направлению
вектора на ) в ряд Тейлора по координате , оставив только члены, независимые и линейные
от .
Считая
справедливой гипотезу малых перемещений (см. п. 1.3.2.1), можно определить поле
по полю 
и вектору
углов поворота 
вектора
нормали 
к осям
г.с.к. . Введем также вектор углов поворота 
вектора
нормали 
вокруг
осей г.с.к. , связанный с формулами:
(1.3.3.1.11)
На
рис. 1.3.3.2 изображены вектора 
и . Вектор нормали поворачивается вокруг направления, задаваемого
вектором , на угол
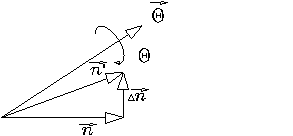
Рис. 1.3.3.2
Изменение вектора 
определяется по формуле:
(1.3.3.1.12)
Поэтому
дополнительное смещение точки , удаленной от точки на вдоль , равно: 
. В результате мы можем записать следующее
выражение для поля вектора перемещений точек
оболочки:
(1.3.3.1.13)
Так
как вектор нормали определяется геометрией поверхности оболочки,
то можно сделать вывод, что поле перемещений точек оболочки однозначно определяется полем перемещений
точек нейтральной поверхности (мембранная составляющая перемещений) и полем вектора
углов поворота 
вектора
нормали вокруг
осей г.с.к. , определяющим изгибную составляющую перемещений. Как и в случае мембраны, поле 
мембранной
составляющей перемещений не зависит от , а изгибная составляющая перемещений линейно
зависит от .
Для
тонкой оболочки должна быть справедлива гипотеза Кирхгоффа (см. п. 1.3.2.1), которая в криволинейных
координатах имеет вид:
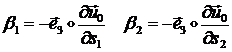(1.3.3.1.14)
Вектор деформации оболочки 
удобно
определять в локальной системе координат точки , задаваемой репером . Компоненты [6]:
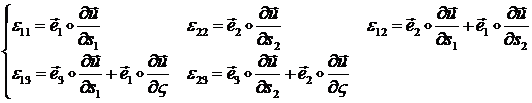
(1.3.3.1.15)
где: 
берется из формулы
(1.3.3.1.13).
Последние две компоненты 
и 
представляют собой
деформацию поперечного сдвига. Как и для пластины (см. п. 1.3.2.2), деформацию
поперечного сдвига можно считать постоянной по толщине пластины:
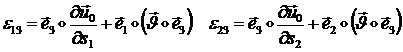(1.3.3.1.16)
Пользуясь формулой (1.3.3.1.11) для связи 
и , можно упростить, например, выражение 
:
Поэтому формулы (1.3.3.1.16) принимают вид:
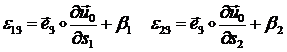(1.3.3.1.17)
В соответствии с формулами Кирхгоффа (1.3.3.1.14) для тонкой оболочки получим из (1.3.3.1.17):
(1.3.3.1.18)
то есть деформации поперечного сдвига для тонкой оболочки
равны нулю. Поэтому остается трехкомпонентный вектор деформаций тонкой оболочки
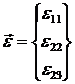, содержащий две составляющие - изгибную и мембранную:
(1.3.3.1.19)
где: 
- мембранная
составляющая деформации тонкой оболочки ;
- изгибная
составляющая деформации тонкой оболочки.
Можно показать, что вектор представим в виде [6]:
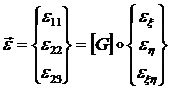(1.3.3.1.20)
где: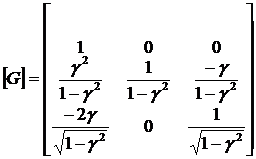 
(1.3.3.1.21)
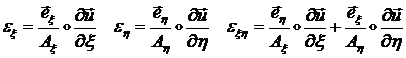(1.3.3.1.22)
Заметим, что из (1.3.3.1.11) следует векторное равенство: 
. Поэтому формулу (1.3.3.1.13) можно привести к виду
(1.3.3.1.23)
аналогичному формулам (1.3.2.1.1) и (1.3.2.1.2) для пластины.
Векторное произведение 
можно представить в
матричном виде:
(1.3.3.1.24)
где: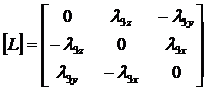 
(1.3.3.1.25)
Тогда с помощью (1.3.3.1.20) - (1.3.3.1.22) получим следующую формулу:
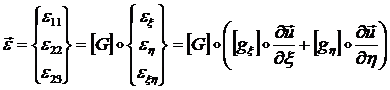(1.3.3.1.26)
где: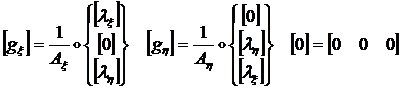 
Учитывая (1.3.3.1.23) для , получим:
(1.3.3.1.27)
где: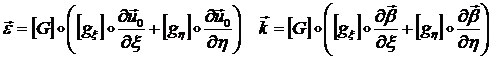 
Таким образом, вектор деформации представим в виде:
(1.3.3.1.28)
где вектора и 
не зависят от
переменной .
Так как и мембранные, и изгибные деформации описываются
плоским напряженным состоянием (см. п. 1.3.1.1 и п. 1.3.2.1), то связь между вектором деформации вектором напряжений 
выражается формулой:
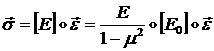(1.3.3.1.29)
где: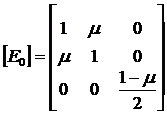 
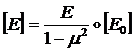- матрица упругости
плоского напряженного состояния.
Поэтому полная энергия деформации тонкой оболочки 
равна:
(1.3.3.1.30)
где: 
- введенная выше
матрица упругости для плоского напряженного состояния.
Интегрирование в (1.3.3.1.30) ведется по всему объему
оболочки. Подставив в формулу (1.3.3.1.30) выражение (1.3.3.1.28) для вектора
деформаций , получим:
Элементарный объем 
представим в виде: 
,
где: 
- элемент поверхности
оболочки. Тогда вследствие разделения интегрирования по и по поверхности
оболочки можно сразу провести интегрирование по . Учитывая равенства:
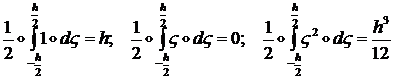
получим выражение для :
(1.3.3.1.31)
Таким образом, полная энергия деформации тонкой оболочки равна сумме энергий мембранной и изгибной деформаций:
(1.3.3.1.32)
где: 
- энергия мембранных деформаций;
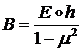- мембранная жесткость
оболочки;
- энергия изгибных
деформаций;
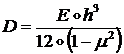- изгибная жесткость
оболочки.
С учетом (1.3.3.1.9) элемент площади равен:
(1.3.3.1.33)
поэтому выражения для энергий деформаций принимают вид:
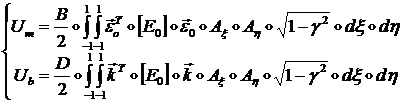(1.3.3.1.34)
где интегрирование ведется по криволинейным координатам .
Изложенная теория тонкой оболочки будет дальше использована для построения различных типов элементов тонкой оболочки. При этом мы снова будем требовать выполнение условия совместности для элементов.
* * *
Для толстой оболочки условия Кирхгоффа (1.3.3.1.14) не
выполняются, поэтому деформации поперечного сдвига 
не равны нулю и определяются
с помощью формул (1.3.3.1.17). Используя соотношения между компонентами
векторов углов поворота 
,
можно представить вектор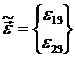 
в следующем виде:
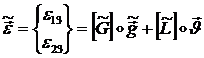(1.3.3.1.35)
где: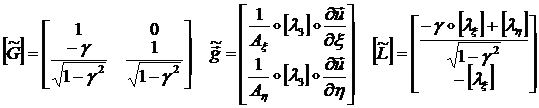 
Полная энергия деформации толстой оболочки будет равна сумме:
(1.3.3.1.36)
где энергия мембранных деформаций и энергия изгибных деформаций определяются по формулам (1.3.3.1.34), а энергия деформаций поперечного сдвига равна:
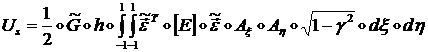(1.3.3.1.37)