1.3.2.2. Четырехугольный изопараметрический элемент тонкой пластины без промежуточных узлов

Понятие изопараметрических элементов было дано в разделе 1.3.2, посвященном элементам мембраны. Там было показано, что изопараметрические элементы являются совместными. Рассмотрим здесь простой четырехугольный изопараметрический элемент пластины, изображенный на рис. 1.3.2.3, имеющий 4 узла в вершинах четырехугольника [6].

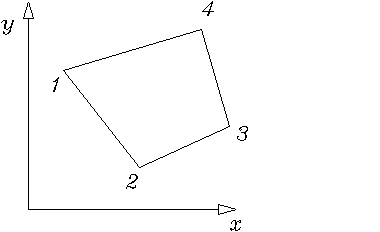
Рис. 1.3.2.3

Как и при рассмотрении элементов мембраны, введем в плоскости квадрат (2x2), изображенный на рис. 1.3.2.4.

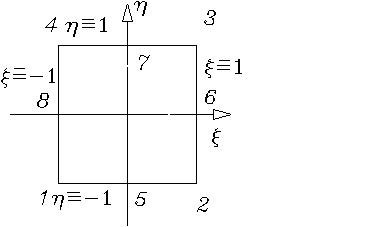
Рис. 1.3.2.4

Геометрия четырехугольника на рис. 1.3.2.3 может быть получена в результате отображения квадрата в плоскости на плоскость с помощью следующих параметрических формул:

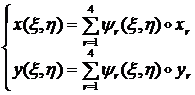(1.3.2.2.1)

где: функции формы , заданы на квадрате в плоскости , являются билинейными по и имеют вид (см. формулу (1.3.1.3.1)):

(1.3.2.2.2)

где: - и координаты узлов .

В качестве независимых функций переменных выберем и , определенные в п. 1.3.2.1. В соответствии с формулами (1.3.2.1.1) и (1.3.2.1.2) эти функции однозначно определяют поле вектора перемещений . Поэтому непрерывность функций и обеспечивает непрерывность перемещений , что означает выполнение условия сходимости.

Здесь все три указанные функции аппроксимируются независимо с помощью тех же самых функций формы :

(1.3.2.2.3)

где: - значение в узле ;

- значение в узле ;

- значение в узле .

Таким образом, данный элемент пластины имеет в каждом узле по 3 степени свободы, так что мы получаем трехкомпонентный вектор степеней свободы узла :

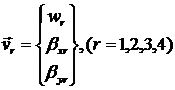(1.3.2.2.4)

Всего у элемента будет 3 x 4 = 12 степеней свободы, поэтому вектор степеней свободы элемента будет иметь 12 компонент:

В действительности же, как мы знаем из теории тонкой пластины (см. п. 1.3.2.1), функции связаны с функцией формулами Кирхгоффа (1.3.2.1.4). Это приводит для данного элемента к появлению ложных деформаций поперечного сдвига , что сильно завышает жесткость на изгиб такого элемента. Оказывается, как и в случае элементов мембраны (см. п. 1.3.1.5), можно эффективно устранять ложные деформации поперечного сдвига пластины путем интегрирования сдвиговой части матрицы жесткости с минимально допустимым порядком интегрирования. Указанная процедура используется для рассматриваемого элемента пластины.

Вектор изгибных деформаций 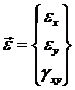будет аппроксимироваться по следующей формуле:

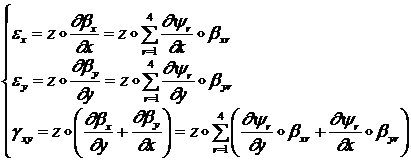(1.3.2.2.5)

или 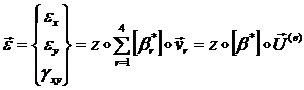(1.3.2.2.6)

где: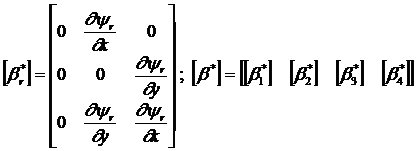

Здесь - матрица деформирования для изгиба.

Вектор деформаций поперечного сдвига 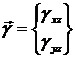будет аппроксимироваться по формулам:

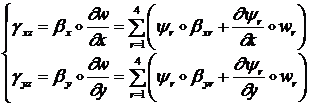(1.3.2.2.7)

или 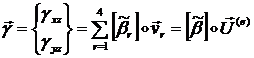(1.3.2.2.8)

где: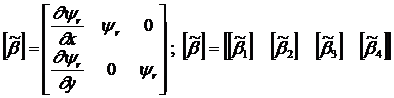

Здесь: - матрица деформирования для поперечного сдвига.

Энергия деформации пластины равна:

(1.3.2.2.9)

где: - энергия изгибных деформаций;

- энергия деформаций поперечного сдвига;

- вектор изгибных деформаций (см. (1.3.2.1.16)).

Подставляя в интегралы (1.3.2.2.9) формулу (1.3.2.2.6) для и формулу (1.3.2.2.8) для , получим:

(1.3.2.2.10)

где: - матрица жесткости элемента;

- матрица жесткости на изгиб;

- матрица жесткости поперечного сдвига.

(Параметры и определены в п. 1.3.2.1.)

Переходя к интегрированию по квадрату в плоскости , получим следующие формулы для матриц жесткости:

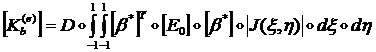
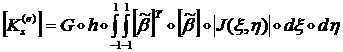(1.3.2.2.11)

Как и в случае мембраны, при вычислении следует проводить интегрирование по Гауссу (2x2), а при вычислении с целью устранения ложных деформаций поперечного сдвига - с минимально допустимым порядком (1x1).

Заметим также, что в соответствии с балочной теорией, сдвиговые деформации меняются по квадратичному закону, а у нас они постоянны по толщине. Поэтому вклад в матрицу жесткости элемента сдвиговых деформаций будет несколько меньше, что можно учесть заменой в формуле (1.3.2.2.11) на (см.: [6]).

Рассмотренный здесь изопараметрический элемент тонкой пластины может быть легко изменен для моделирования толстой пластины, определение которой было дано в конце п. 1.3.2.1. Для этого достаточно сохранить в формулах (1.3.2.2.11), определяющих матрицы жесткости и , интегрирование по Гауссу (2 х 2) для обеих матриц.