1.3.2 Элементы пластины

1.3.2.1 Понятие пластины. Теория тонкой пластины

ОПРЕДЕЛЕНИЕ

Пластиной будем называть такой плоский двумерный элемент, который воспринимает действие сил из плоскости элемента, а также действие моментов сил относительно осей, лежащих в плоскости элемента.

Под действием указанных силовых факторов пластина может изгибаться, испытывая неравномерное смещение своих точек из плоскости (недеформированного состояния пластины). Здесь мы рассмотрим теорию тонкой пластины, толщина которой много меньше характерного размера пластины вдоль двух других направлений [8].

Изгиб пластины будем считать малым, то есть смещения точек пластины много меньше ее толщины . При изгибе на выпуклой стороне пластины возникает растяжение, а на вогнутой - сжатие.

Поэтому где-то внутри пластины должна существовать нейтральная поверхность, на которой отсутствуют деформации, а по двум сторонам от нее деформации имеют противоположный знак.

Выберем декартову систему координат с началом в т. O на нейтральной поверхности и осью , нормальной к этой поверхности. Нейтральная поверхность будет тогда лежать в плоскости (рис. 1.3.2.1).

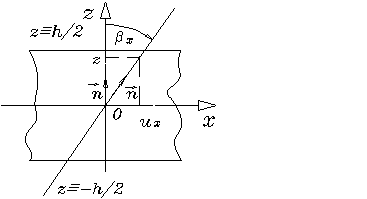
Рис. 1.3.2.1

Пусть: - вектор перемещения точки пластины с декартовыми координатами .

Так как перемещения точек пластины малы по сравнению с ее толщиной , то можно сохранить лишь первые неисчезающие члены разложения в ряд Тейлора поля вектора перемещения по координате . Именно, перемещения точек из плоскости пластины вдоль оси можно считать постоянными (независящими от ) и равными соответствующим перемещениям вдоль оси точек нейтральной поверхности:

(1.1.3.1)

Перемещения же точек вдоль осей и можно считать линейно зависящими от . Здесь полезна следующая геометрическая иллюстрация (рис. 1.3.2.1). При малых деформациях отрезок оси , принадлежащий пластине, переходит в отрезок же, т. е. поворачивается как целое, например, к оси на малый угол .

Единичный направляющий вектор оси повернется на угол к оси и на угол к оси . Тогда, как легко может быть понято из рис. 1.3.2.1, перемещения точек пластины вдоль осей и могут быть определены по следующим формулам:

(1.3.2.1.2)

Формула (1.3.2.1.1) и (1.3.2.1.2) составляют содержание так называемой гипотезы малых перемещений точек пластины.

Кроме вектора углов поворота вектора нормали к поверхности пластины к осям и , введем вектор углов поворота вектора нормали вокруг осей и в соответствии с правилами вращения для правой системы координат , указанными на рис. 1.3.2.2.

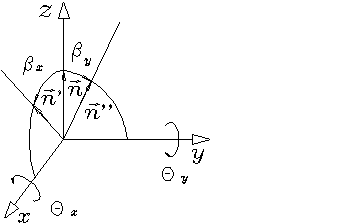
Рис. 1.3.2.2

Из рис. 1.3.2.2 следует связь между и :

(1.3.2.1.3)

Кроме гипотезы малых перемещений, для тонкой пластины справедлива гипотеза Кирхгоффа, утверждающая, что вектор нормали недеформированной поверхности пластины остается вектором нормали и к деформированной поверхности. Простейшее геометрическое рассмотрение этой гипотезы дает следующую дифференциальную связь между смещениями точек вдоль оси и углами поворота к осям и :

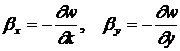(1.3.2.1.4)

Формулы (1.3.2.1.4) называются условиями Кирхгоффа для тонкой пластины. В соответствии с общей формулой (1.1.1.11), граничные условия на поверхности пластины имеют вид

(1.3.2.1.5)

где: - тензор напряжений:

- вектор нормали к поверхности;

- вектор внешних сил на единицу площади поверхности пластины.

Силы , вообще говоря, действуют на поверхности пластины, но эти силы, во всяком случае, должны быть для тонкой пластины много меньше внутренних напряжений . Поэтому их можно считать равными нулю; тогда граничные условия для пластины примут вид:

(1.3.2.1.6)

Так как вектор нормали направлен в нашем случае вдоль оси , то единственная отличная от нуля его компонента: .

Поэтому формула (1.3.2.1.6) принимает вид:

(1.3.2.1.7)

Учитывая формулы (1.1.1.6) связи компонент вектора напряжений с компонентами вектора деформаций , формулу (1.3.2.1.7) можно записать в виде:

(1.3.2.1.8)

Так как пластина тонкая, то эти условия можно считать справедливыми по всей толщине пластины. Заметим, что граничные условия (1.3.2.1.8) полностью совпадают с условиями для плоского напряженного состояния (1.3.1.1.1) и (1.3.1.1.1).

Поэтому по аналогии с п. 1.3.1.1 можно ввести трехкомпонентные вектора изгибных деформаций и изгибных напряжений и связь между ними:

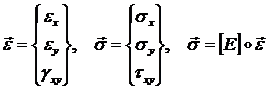(1.3.2.1.9)

где: 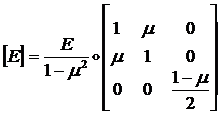- изгибная матрица упругости.

С помощью (1.3.2.1.2) компоненты вектора изгибных деформаций запишутся в виде:

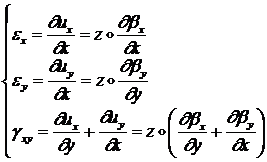(1.3.2.1.10)

Компоненты вектора сдвиговых деформаций 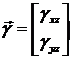с помощью (1.3.2.1.1) и (1.3.2.1.2) примут вид:

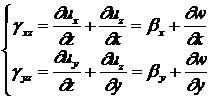(1.3.2.1.11)

В соответствии с условиями Кирхгоффа (1.3.2.1.4) для тонкой пластины получим из (1.3.2.1.11):

(1.3.2.1.12)

то есть сдвиговые деформации для тонкой пластины равны нулю.

Получим, наконец, выражение для полной энергии деформации пластины [6]. В общем случае эта энергия равна:

(1.3.2.1.13)

где: - энергия изгибной деформации пластины;

- энергия сдвиговой деформации пластины;

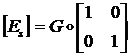- сдвиговая матрица упругости.

В соответствии с (1.3.2.1.10) вектор изгибных деформаций можно представить в виде:

(1.3.2.1.14)

где: 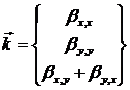- не зависит от .

Из формул (1.3.2.1.11) видно, что вектор деформаций поперечного сдвига 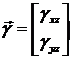не зависит от .

Сделанные выводы о характере зависимости векторов и от позволяют провести в (1.3.2.1.13) интегрирование по .

Учитывая равенства

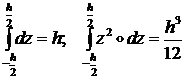
получим выражение для энергий изгибной и сдвиговой деформаций пластины:

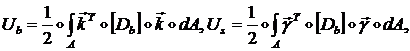(1.3.2.1.15)

где:

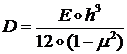- изгибная жесткость пластины ;

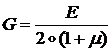- модуль сдвига.

В другом виде энергии деформации можно записать:

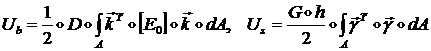(1.3.2.1.16)

В случае тонкой пластины деформации поперечного сдвига равны нулю (см. формулу (1.3.2.1.12)), поэтому:

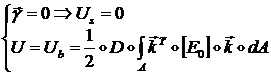(1.3.2.1.17)

Обратим внимание на линейный закон изменения изгибных деформаций по толщине пластины. Этим фактом изгибные деформации пластины существенно отличаются от мембранных деформаций, которые постоянны по толщине пластины. Рассмотренная здесь теория тонкой пластины будет использована дальше при формулировке различных типов элементов тонкой пластины. При этом мы всегда будем требовать от элементов важного в МКЭ условия совместности.