1.3.1.6. Треугольный гибридный элемент мембраны
Гибридные элементы в механике строятся на основе так
называемой дополнительной энергии ![]() [3]:
[3]:
![]() (1.3.1.6.1)
(1.3.1.6.1)
где: ![]() - энергия деформации
элемента, выраженная через внутренние силовые факторы, действующие в элементе;
- энергия деформации
элемента, выраженная через внутренние силовые факторы, действующие в элементе;
![]() - работа внутренних
силовых факторов на границе элемента.
- работа внутренних
силовых факторов на границе элемента.
Варьируемый потенциал ![]() имеет вид (сравните с
п. 1.1.1):
имеет вид (сравните с
п. 1.1.1):
![]() (1.3.1.6.2)
(1.3.1.6.2)
где: ![]() - работа заданных
внешних сил.
- работа заданных
внешних сил.
При этом в вариационном принципе для гибридных элементов варьируется как степени свободы (в общем случае - перемещения и углы поворота), так и внутренние силовые факторы.
Рассмотрим произвольную мембрану, расположенную в плоскости ![]() глобальной декартовой
системы координат
глобальной декартовой
системы координат ![]() .
.
Пусть: 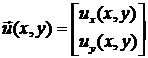 - поле перемещений
мембраны;
- поле перемещений
мембраны;
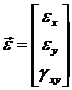 - поле деформаций
мембраны;
- поле деформаций
мембраны;
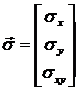 - поле напряжений
мембраны.
- поле напряжений
мембраны.
Напряжения ![]() являются внутренними
силовыми факторами мембраны и связаны с деформациями
являются внутренними
силовыми факторами мембраны и связаны с деформациями ![]() формулой:
формулой:
![]() (1.3.1.6.3)
(1.3.1.6.3)
где: ![]() - матрица упругости
для плоского напряженного состояния (см. п. 1.3.1.1).
- матрица упругости
для плоского напряженного состояния (см. п. 1.3.1.1).
Энергия деформации мембраны ![]() определяется формулой
(1.3.1.1.6):
определяется формулой
(1.3.1.1.6):
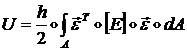 (1.3.1.6.4)
(1.3.1.6.4)
где интегрирование ведется по поверхности мембраны (кроме
боковой поверхности); ![]() - толщина мембраны.
- толщина мембраны.
Воспользовавшись формулой (1.3.1.6.3), выразим энергию
деформации ![]() через внутренние
силовые факторы мембраны
через внутренние
силовые факторы мембраны ![]() :
:
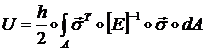 (1.3.1.6.5)
(1.3.1.6.5)
Здесь мы воспользовались симметричностью матрицы упругости: ![]()
Рассмотрим элемент боковой поверхности ![]() с вектором внешней по
отношению к элементу нормали
с вектором внешней по
отношению к элементу нормали ![]() (рис. 1.3.1.8).
(рис. 1.3.1.8).
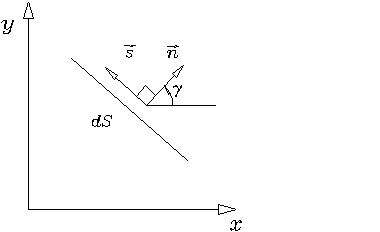
Рис. 1.3.1.8
Единичный вектор ![]() направлен вдоль
элемента
направлен вдоль
элемента ![]() в соответствии с обходом элемента против
часовой стрелки.
в соответствии с обходом элемента против
часовой стрелки.
Элемент ![]() , где:
, где: ![]() - длина элемента.
- длина элемента.
Тогда работа внутренних силовых факторов ![]() равна:
равна:
![]() (1.3.1.6.6)
(1.3.1.6.6)
где интегрирование ведется по границе элемента ![]() ;
;
![]() и
и ![]() - компоненты
- компоненты ![]() , действующие на элементе
, действующие на элементе ![]() вдоль нормали
вдоль нормали ![]() и касательного вектора
и касательного вектора
![]() соответственно.
соответственно.
Поэтому дополнительная энергия мембраны ![]() равна:
равна:
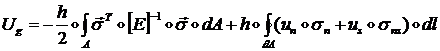 (1.3.1.6.7)
(1.3.1.6.7)
Полученные выражения для дополнительной энергии мембраны используются при построении различных типов гибридных элементов мембраны. Рассмотрим здесь простейший треугольный гибридный элемент мембраны, представляющий собой произвольный треугольник с тремя узлами в его вершинах (рис. 1.3.1.9).
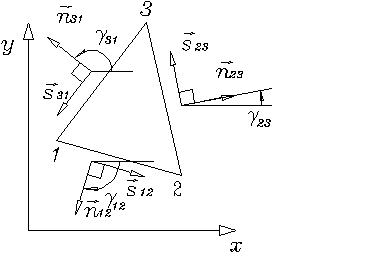
Рис. 1.3.1.9
![]()
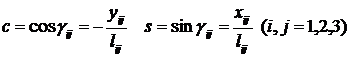
В каждом узле по две степени свободы - перемещения ![]()
![]() вдоль осей
вдоль осей ![]() и
и ![]() соответственно:
соответственно:
Вектор степеней свободы узла ![]() имеет две компоненты:
имеет две компоненты:
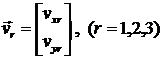
Вектор степеней свободы элемента ![]() имеет 3x3=9 компонент:
имеет 3x3=9 компонент:
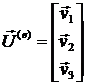
Для треугольного
элемента мембраны поле перемещений ![]() аппроксимируется по
узловым значениям
аппроксимируется по
узловым значениям ![]() линейными по
линейными по ![]() полиномами (см. п. 1.3.1.2).
полиномами (см. п. 1.3.1.2).
Поэтому поле деформаций ![]() , а с ним и поле напряжений
, а с ним и поле напряжений ![]() являются константными.
являются константными.
Поэтому потребуем, чтобы напряжения ![]() для треугольного
гибридного элемента мембраны также были постоянными.
для треугольного
гибридного элемента мембраны также были постоянными.
Тогда энергия деформации (1.3.1.6.5) принимает вид:
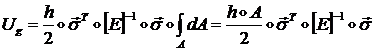 (1.3.1.6.8)
(1.3.1.6.8)
где: ![]() - площадь
треугольника.
- площадь
треугольника.
Рассмотрим теперь интеграл работы ![]() :
:
![]()
Представим его в виде суммы интегралов по трем ребрам элемента:
![]() (1.3.1.6.9)
(1.3.1.6.9)
где: ![]() - длина ребра
- длина ребра ![]() (см. рис. 1.3.1.9):
(см. рис. 1.3.1.9):
Пусть: ![]() - угол между осью
- угол между осью ![]() и нормалью
и нормалью ![]() .
.
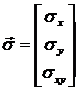 - компоненты
симметричного тензора второго ранга в системе координат
- компоненты
симметричного тензора второго ранга в системе координат ![]() , а
, а
![]() - компоненты того же
тензора в системе координат
- компоненты того же
тензора в системе координат ![]() , повернутой относительно
, повернутой относительно ![]() на угол
на угол ![]() .
.
Закон преобразования компонент симметричного тензора второго ранга следующий:
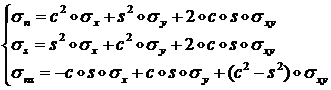 (1.3.1.6.10)
(1.3.1.6.10)
Представим столбец 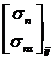 для ребра
для ребра ![]() в виде:
в виде:
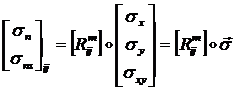 (1.3.1.6.11)
(1.3.1.6.11)
С помощью (1.3.1.6.10) получим следующий вид матрицы ![]()
![]() :
:
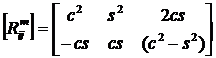 (1.3.1.6.12)
(1.3.1.6.12)
Представим столбец ![]() для ребра
для ребра ![]() в виде:
в виде:
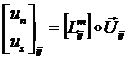 , где
, где ![]() (1.3.1.6.13)
(1.3.1.6.13)
Так как ![]() - компоненты вектора
- компоненты вектора ![]() , то закон преобразования при повороте на угол
, то закон преобразования при повороте на угол ![]() следующий:
следующий:
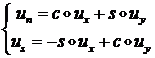 (1.3.1.6.14)
(1.3.1.6.14)
Кроме того, мы будем предполагать линейный закон изменения
перемещений вдоль каждого ребра ![]() :
:
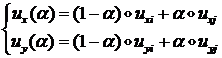 (1.3.1.6.15)
(1.3.1.6.15)
где: ![]() - параметр, непрерывно
меняющийся вдоль ребра (в узле
- параметр, непрерывно
меняющийся вдоль ребра (в узле ![]() , а в узле
, а в узле ![]() ).
).
С помощью формул (1.3.1.6.14) и (1.3.1.6.15) можно
получить следующий вид матрицы ![]() :
:
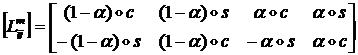 (1.3.1.6.16)
(1.3.1.6.16)
Тогда работа ![]() будет равна:
будет равна:
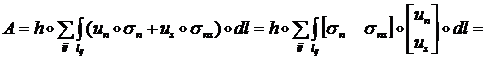
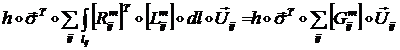 (1.3.1.6.17)
(1.3.1.6.17)
Здесь введена матрица:
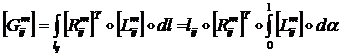 (1.3.1.6.18)
(1.3.1.6.18)
так как: ![]()
Если ![]() - вектор степеней
свободы элемента, то сумму
- вектор степеней
свободы элемента, то сумму ![]() можно представить в
виде:
можно представить в
виде:
![]()
Учитывая значения интегралов 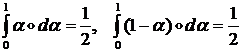 и тождество
и тождество ![]() , можно получить следующее выражение для матрицы
, можно получить следующее выражение для матрицы ![]() :
:
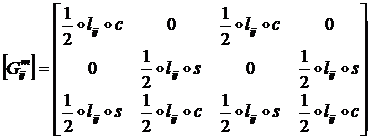 (1.3.1.6.19)
(1.3.1.6.19)
Учитывая формулы: ![]()
Найдем с помощью (1.3.1.6.19) матрицу ![]() :
:
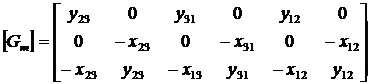 (1.3.1.6.20)
(1.3.1.6.20)
Работа ![]() будет равна:
будет равна: ![]()
Поэтому окончательное выражение для дополнительной энергии ![]() следующее:
следующее:
![]() (1.3.1.6.21)
(1.3.1.6.21)
В соответствии с вариационным принципом для гибридных
элементов, зафиксируем вектор степеней свободы элемента ![]() и будем варьировать
и будем варьировать ![]() , ища истинное значение вектора напряжений
, ища истинное значение вектора напряжений ![]() :
:
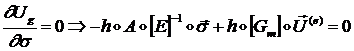 или
или
![]() (1.3.1.6.22)
(1.3.1.6.22)
Заметим, что из (1.3.1.6.22) следует:
![]() (1.3.1.6.23)
(1.3.1.6.23)
где введена матрица жесткости гибридного элемента ![]() :
:
![]() (1.3.1.6.24)
(1.3.1.6.24)
Из формулы (1.3.1.6.20) легко заметить, что матрица ![]() связана с матрицей
деформирования
связана с матрицей
деформирования ![]() (1.3.1.2.11) для
элемента мембраны из п. 1.3.1.2 формулой:
(1.3.1.2.11) для
элемента мембраны из п. 1.3.1.2 формулой:
![]() (1.3.1.6.25)
(1.3.1.6.25)
Поэтому окончательно матрица жесткости построенного
гибридного элемента ![]() равна:
равна:
![]() (1.3.1.6.26)
(1.3.1.6.26)
т.е. полностью совпадает с матрицей жесткости элемента мембраны (1.3.1.2.13) из п. 1.3.1.2.
Полученное совпадение матрицы жесткости изопараметрического и гибридного треугольных элементов уже не имеет места при переходе к четырехугольному элементу. Этому вопросу посвящен следующий пункт 1.3.1.7.