1.3 Двумерные элементы
1.3.1 Элементы мембраны
1.3.1.1 Понятие мембраны. Плоское напряженное состояние
После того, как мы рассмотрели элементы стержня, являющиеся одномерными, мы перейдем к изучению двумерных элементов. Изучение двумерных элементов в механике мы начнем с простейшего типа - элементов мембраны.
ОПРЕДЕЛЕНИЕ
Мембраной мы будем называть такой плоский двумерный элемент, который может испытывать действие сил только в его плоскости.
Мембранами моделируются достаточно тонкие металлические пластинки, испытывающие растяжение или сжатие в своей плоскости.
Пусть декартовая система координат выбрана таким образом,
что мембрана лежит в плоскости ![]() , а ось
, а ось ![]() перпендикулярна к
плоскости мембраны.
перпендикулярна к
плоскости мембраны.![]()
Пусть ![]() и
и ![]() - вектора напряжения
и деформации мембраны соответственно.
- вектора напряжения
и деформации мембраны соответственно.
Из соображений симметрии следует, что:
![]() (1.3.1.1.1a)
(1.3.1.1.1a)
Так как на поверхности мембраны (за исключением боковой поверхности) нет никаких сил, то:
![]() (1.3.1.1.1b)
(1.3.1.1.1b)
Поэтому если мембрана тонкая (а это предполагается справедливым), то условие (1.3.1.1.1) можно
считать выполненным по всей толщине
мембраны. Описанное напряженное состояние называют в механике плоским напряженным
состоянием. С помощью формул (1.1.1.6)
можно установить связь компонент вектора деформаций ![]() с компонентами вектора
напряжений
с компонентами вектора
напряжений ![]() :
:
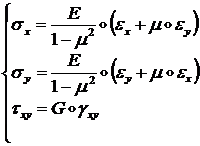 (1.3.1.1.2)
(1.3.1.1.2)
Что касается деформаций мембраны вдоль оси ![]() , то имеем:
, то имеем:
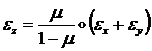
то есть ![]() является функцией от
является функцией от ![]() и
и ![]() . В МКЭ для двухмерных
элементов деформации из поверхности элемента не рассматриваются.
. В МКЭ для двухмерных
элементов деформации из поверхности элемента не рассматриваются.
Поэтому мы вправе для описания плоского напряженного состояния пользоваться трехкомпонентными векторами:
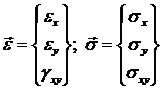 (1.3.1.1.3)
(1.3.1.1.3)
Эти вектора связаны друг с другом матрицей упругости ![]() :
:
![]() , где
, где 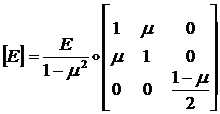 (1.3.1.1.4)
(1.3.1.1.4)
Энергия деформации мембраны будет иметь вид:
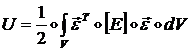 (1.3.1.1.5)
(1.3.1.1.5)
где интегрирование ведется по всему объему мембраны.
Так как мембрана плоская и предполагается постоянной толщины
![]() , то:
, то:
 (1.3.1.1.6)
(1.3.1.1.6)
где интегрирование ведется по поверхности мембраны (кроме боковой поверхности).
1.3.1.2 Треугольный элемент мембраны без промежуточных узлов
Рассмотрим сначала простейший элемент мембраны,
представляющий собой произвольный треугольник (рис. 1.3.1.1) с тремя узлами ![]() в его вершинах [6]. В
[ИСПА] тип этого конечного элемента -
40.
в его вершинах [6]. В
[ИСПА] тип этого конечного элемента -
40.
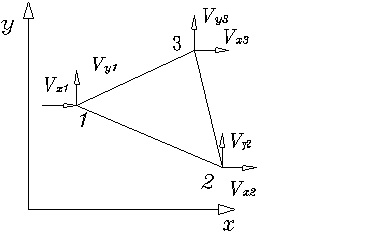
Рис. 1.3.1.1
Перемещения ![]() вдоль осей
вдоль осей ![]() и
и ![]() в i-ом узле элемента
мембраны представляют собой его степени свободы, которых у мембраны в каждом
узле по две.
в i-ом узле элемента
мембраны представляют собой его степени свободы, которых у мембраны в каждом
узле по две.
Итого у треугольного элемента мембраны 6 степеней свободы.
Обозначим через
вектор степеней свободы (перемещений) в узле ![]() :
:
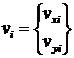 , (
, (![]() = 1,2,3), (1.3.1.2.1)
= 1,2,3), (1.3.1.2.1)
а через ![]() - вектор степеней
свободы элемента:
- вектор степеней
свободы элемента:
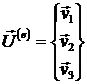 (1.3.1.2.2)
(1.3.1.2.2)
Вектор ![]() имеет сейчас 6
компонент.
имеет сейчас 6
компонент.
Пусть: ![]() - поле перемещений в пределах треугольной мембраны. Так как аппроксимация
ведется по трем значениям
- поле перемещений в пределах треугольной мембраны. Так как аппроксимация
ведется по трем значениям ![]() в узлах элемента, то
поле перемещений
в узлах элемента, то
поле перемещений ![]() в треугольном элементе
может быть представлено с помощью полного линейного полинома:
в треугольном элементе
может быть представлено с помощью полного линейного полинома:
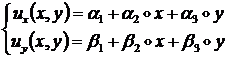 (1.3.1.2.3)
(1.3.1.2.3)
В вершинах треугольника значения функций из (1.3.1.2.3)
должны совпадать с узловыми перемещениями ![]() (
(![]() = 1,2,3).
= 1,2,3).
Легко понять, что функции (1.3.1.2.3) могут быть записаны в виде:
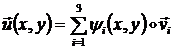 (1.3.1.2.4)
(1.3.1.2.4)
где: ![]() ; (
; (![]() = 1,2,3) - функции формы треугольного элемента, причем:
= 1,2,3) - функции формы треугольного элемента, причем:
1) ![]() - линейные полиномы;
- линейные полиномы;
2) ![]() обращаются в узле
обращаются в узле ![]() в единицу, если
в единицу, если ![]() , и в ноль, если
, и в ноль, если ![]()
3) 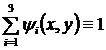 - общее свойство функций формы.
- общее свойство функций формы.
Последнее свойство обеспечивает перемещение элемента как целого. Можно показать, что эти функции формы имеют следующие свойства [4]:
1) Функции ![]() имеют вид:
имеют вид:
![]() , где
, где
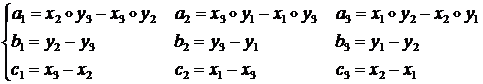
(1.3.1.2.5)
Здесь: ![]() - площадь треугольника, которая может быть вычислена по
формуле:
- площадь треугольника, которая может быть вычислена по
формуле:
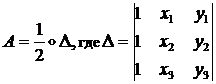 - определитель. (1.3.1.2.6)
- определитель. (1.3.1.2.6)
2) Интеграл вдоль ребра 1-2 треугольника:
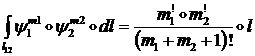 (1.3.1.2.7)
(1.3.1.2.7)
Здесь ![]() длина ребра 1-2; для
ребер 2-3 и 3-1 аналогично.
длина ребра 1-2; для
ребер 2-3 и 3-1 аналогично.
3) Интеграл по площади треугольника:
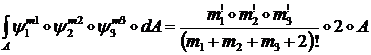 (1.3.1.2.8)
(1.3.1.2.8)
Зная поле перемещений ![]() из (1.3.1.2.4), мы
можем найти поле деформаций
из (1.3.1.2.4), мы
можем найти поле деформаций ![]() :
:
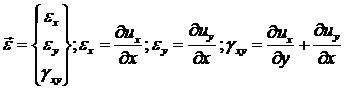 (1.3.1.2.9)
(1.3.1.2.9)
С помощью (1.3.1.2.4) получим:
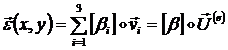 где матрицы: (1.3.1.2.10)
где матрицы: (1.3.1.2.10)
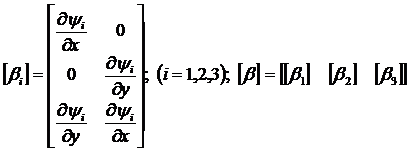
Матрица ![]() , определяющая поле вектора деформаций элемента по вектору
степеней свободы
, определяющая поле вектора деформаций элемента по вектору
степеней свободы ![]() элемента называется
матрицей деформирования. Согласно (1.3.1.2.5), матрица
элемента называется
матрицей деформирования. Согласно (1.3.1.2.5), матрица ![]() имеет вид:
имеет вид:
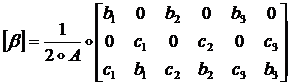 (1.3.1.2.11)
(1.3.1.2.11)
Тогда энергия деформации элемента примет вид:
![]() (1.3.1.2.12)
(1.3.1.2.12)
где: ![]()
В нашем случае матрица деформирования ![]() имеет размерность
(3x6), а матрица жесткости
имеет размерность
(3x6), а матрица жесткости ![]() имеет размерность
(6x6).
имеет размерность
(6x6).
Так как матрица ![]() в (1.3.1.2.11)
постоянна, то из (1.3.1.2.12) следует, что матрица жесткости треугольного
элемента мембраны имеет вид:
в (1.3.1.2.11)
постоянна, то из (1.3.1.2.12) следует, что матрица жесткости треугольного
элемента мембраны имеет вид:
![]() (1.3.1.2.13)
(1.3.1.2.13)
Покажем теперь, как находить узловые силы.
Работа объемных сил ![]() согласно (1.1.1.14) равна:
согласно (1.1.1.14) равна:
![]()
Но из (1.3.1.2.4) следует, что: 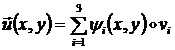
Поэтому работу ![]() можно представить в
виде:
можно представить в
виде:
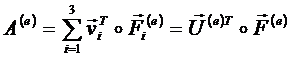
где: ![]() - узловая сила в i-ом
узле элемента;
- узловая сила в i-ом
узле элемента;
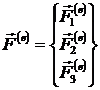 -вектор силовых
факторов элемента.
-вектор силовых
факторов элемента.
Так как согласно (1.3.1.2.12) 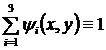 , то:
, то:
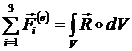
Функционал ![]() для элемента тогда
примет стандартный вид:
для элемента тогда
примет стандартный вид:
![]()
После варьирования получим уравнения равновесия элемента:
![]()
После перехода к глобальным величинам ![]() получим глобальные
уравнения равновесия:
получим глобальные
уравнения равновесия: ![]() .
.