1.2.3 Применение общей теории МКЭ для построения стержня с постоянным по длине сечением

Как и в п. 1.2.2, рассмотрим прямой стержень с постоянным по длине сечением (рис. 1.2.1). В п. 1.2.2 для такого стержня был построен конечный элемент с двумя узлами на его концах (тип 000).

Конечный элемент был построен на основе балочной теории стержня.

Оказывается, этот же элемент стержня можно построить на основе рассмотренной в разделе 1.1 общей теории МКЭ.

Как и в п. 1.2.2, определим для каждого узла стержня (=1,2) вектор перемещений , вектор углов поворота , вектор сил и вектор моментов сил . В пределах элемента все величины, относящиеся к элементу , будем аппроксимировать с помощью функций формы по их значениям в узлах.

Для построения конечного элемента стержня необходимо построить функционал (см. п. 1.1.1):

где: - работа внешних сил, приложенных к стержню;

- энергия (малых) деформаций стержня.

Далее мы используем известные результаты теории упругости [8] и теории сопротивления материалов [9] для растяжения-сжатия, кручения и изгиба стержня.

Энергия (малых) деформаций стержня равна:

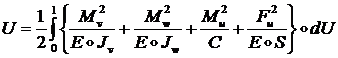(1.2.3.1)

где: - модуль упругости;

- моменты инерций сечения относительно (главных) осей и соответственно;

- крутильная жесткость стержня (в случае круглого сечения стержня: , где - полярный момент инерции);

- площадь сечения стержня.

Для всего стержня мы будем иметь поля вектора перемещений и вектора углов поворота .

В балочной теории стержня определялись на основе дифференциальных уравнений изогнутой оси балки (см. п. 1.2.2).

В МКЭ неизвестные величины (в данном случае - ) аппроксимируются в пределах каждого конечного элемента по их узловым значениям (в данном случае - ) с помощью функций формы, заданных на конечном элементе.

Так как в случае справедливости закона Гука уравнения теории упругости являются линейными, то справедлив принцип суперпозиции, согласно которому результирующее действие всех силовых факторов, приложенных к конструкции (стержню) может быть определено как сумма (суперпозиция) действий каждого отдельного силового фактора.

В соответствии с известными формулами имеем (сравните с п. 1.2.2):

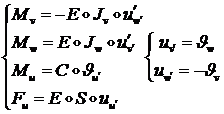(1.2.3.2)

(Штрих означает дифференцирование по ).

Поэтому окончательно энергия деформации стержня принимает вид:

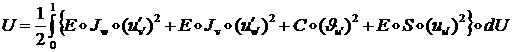
(1.2.3.3)

Мы видим, что равна суперпозиции энергий деформаций, связанных с изгибом относительно осей и , кручением относительно оси и растяжением (сжатием) относительно оси .

Работа внешних сил равна:

(1.2.3.4)

Теперь нам осталось только построить аппроксимацию полей векторов и на элементе.

Введем безразмерную переменную по формуле:

где - длина стержня.

Тогда:

Мы видим, что в (1.2.3.3) компоненты дифференцируются дважды по , а - один раз. Поэтому очевидно, что самой простейшей полиномиальной аппроксимацией в первом случае будет квадратичная, а во втором - линейная.

Линейная аппроксимация требует 2-х параметров, а квадратичная - трех. Так как число узлов у стержня два (1 и 2), то число параметров должно быть четным: четыре в первом и два во втором случае.

Итак, мы пришли к выводу, что самый простой элемент стержня с двумя узлами требует линейной аппроксимации для и кубической аппроксимации для (соответственно, будут меняться, как следует из (1.2.3.2), по квадратичному закону).

Линейные полиномы.

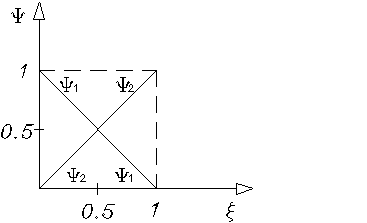
Рис. 1.2.6

Линейные полиномы, изображенные на рис. 1.2.6, могут быть аналитически описаны следующим образом:

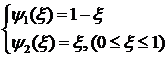(1.2.3.5)

при этом:

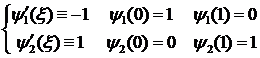
(штрих означает дифференцирование по ).

Тогда аппроксимация имеет вид:

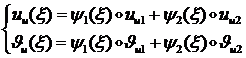(1.2.3.6)

Если ввести векторы: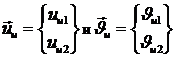

и матрицу функций формы: то формулы (1.2.3.6) примут вид:

(1.2.3.7)

Кубические полиномы

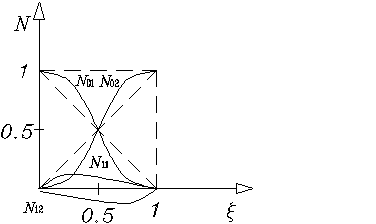
Рис. 1.2.7

Кубические полиномы изображены на рис. 1.2.7.

Аппроксимация кубических полиномов имеет следующий вид:

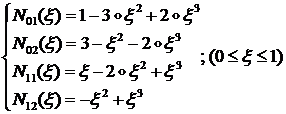(1.2.3.8)

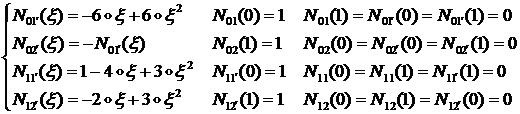
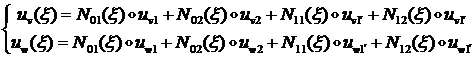(1.2.3.9)

Если ввести векторы: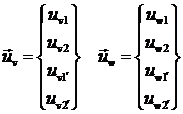

и матрицу функций формы: то формулы (1.2.3.9) примут вид:

(1.2.3.10)

Подставив аппроксимирующие формулы (1.2.3.7) и (1.2.3.10) в формулу (1.2.3.3), для энергии деформации получим выражение:

где:

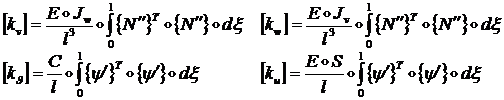
(1.2.3.11)

(индекс - означает операцию транспонирования, поэтому, например, если: - вектор-столбец, то - вектор-строка).

Вычисление интегралов в (1.2.3.11) дает:

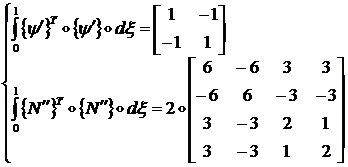(1.2.3.12)

Полученные в (1.2.3.11) матрицы: - называются матрицами жесткости стержневого элемента, работающего только на изгиб относительно оси , изгиб относительно оси , кручение относительно оси и растяжение-сжатие вдоль оси соответственно.

С учетом соотношений (см. 1.2.3.2):

(штрих означает дифференцирование по ).

окончательно получим следующее выражение для матриц жесткости и энергии деформации:

где:

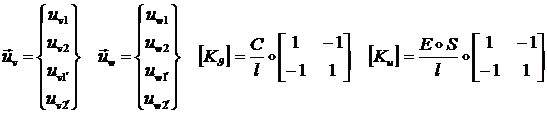
(1.2.3.13)

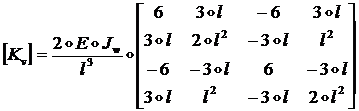
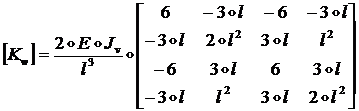
Сравнение формул (1.2.3.13) и (1.2.2.30)-(1.2.2.32) указывает на полное совпадение выражений для матриц жесткости . Это доказывает сделанное в начале этого пункта утверждение, что элемент стержня типа 000 можно построить на основе общей теории МКЭ.

Причина указанного совпадения в том, что аппроксимация неизвестных величин (линейная для и кубическая для ) дает точные аналитические выражения, полученные по балочной теории стержня. Действительно, в п. 1.1.2 установлено, что перемещение и угол поворота меняются по линейному закону, а перемещения - по кубическому.

Рассмотрим теперь произвольную конструкцию, состоящую из стержней. Если все стержни прямые и постоянного сечения, то каждый стержень в МКЭ мы можем теперь заменить на один конечный элемент с двумя узлами. Если же некоторые из стержней конструкции не являются прямыми или же имеют переменные по длине сечения, то такие стержни мы разбиваем на несколько стержневых элементов.