1.2.2 Элемент стержня с постоянным по длине сечением по балочной теории
Рассмотрим конечный элемент прямого стержня с постоянным по длине сечением с двумя узлами 1 и 2 на его концах (рис. 1.2.1). Тип элемента в [ИСПА] - 000. В п. 1.2.1 была рассмотрена балочная теория такого стержня.
В каждом узле элемента по 6 степеней свободы: три
перемещения 
и три угла поворота 
. Вектор степеней свободы узла 
имеет тогда 6
компонент
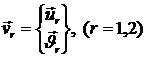
а вектор степеней свободы элемента 
имеет 6х2 = 12
компонент:
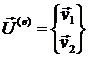
Вектор силовых факторов в узле 
имеет 6 компонент: три
силы 
и три момента сил 
, а вектор силовых факторов элемента 
имеет 12 компонент:
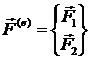
Матрица жесткости элемента 
будет иметь
размерность (12х12). Уравнение связи вектора силовых факторов элемента и вектора степеней
свободы элемента будет иметь вид:
(1.2.2.1)
Как известно из п. 1.2.1, для силовых факторов стержневого
элемента справедлив принцип суперпозиции. Поэтому матрицу жесткости элемента
стержня можно представить в виде суммы матриц жесткости:
1) 
- для растяжения
(сжатия) вдоль оси 
;
2) 
- для кручения
относительно оси ;
3) 
- для изгиба
относительно оси 
;
4) 
- для изгиба
относительно оси 
.
Рассмотрим последовательно четыре деформированных состояния
стержня и получим для них матрицы жесткости: 
. Тем самым задача нахождения матрицы жесткости стержня будет
решена.
МАТРИЦА ЖЕСТКОСТИ ДЛЯ
РАСТЯЖЕНИЯ (СЖАТИЯ)
Пусть: 
- перемещения узлов 1
и 2 вдоль оси ;
- силы в узлах 1 и 2,
действующие вдоль оси .
Тогда вектор силовых факторов 
будет связан с вектором степеней свободы 
с помощью матрицы
жесткости 
, имеющей размерность (2х2):
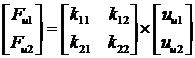(1.2.2.2)
Условие равновесия
элемента для растяжения (сжатия) вдоль оси имеет вид:
(1.2.2.3)
Пусть сначала 
. Тогда из (1.2.2.2) и (1.2.2.3) следует, что: 
. Но из (1.2.1.2) следует, что:
.
Поэтому заключаем, что: 
.
Аналогичное рассмотрение случая 
дает: 
. Поэтому матрица жесткости имеет следующий вид:
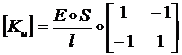(1.2.2.4)
МАТРИЦА ЖЕСТКОСТИ
КРУЧЕНИЯ
Пусть:
- углы поворота сечений в узлах 1 и 2 относительно оси ;
- моменты сил в узлах
1 и 2 относительно оси .
Тогда матрица жесткости, имеющая размерность (2х2), связывает вектор силовых факторов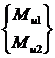 
с вектором степеней
свободы 
уравнением:
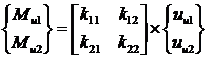(1.2.2.5)
Уравнение равновесия элемента для кручения относительно оси имеет вид:
(1.2.2.6)
Пусть сначала 
. Тогда из (1.2.2.5) и (1.2.2.6) следует, что: 
. Из (1.2.1.14) следует, что:
.
Поэтому: 
. Аналогичным образом находим, что: 
.
Поэтому матрица жесткости имеет вид:
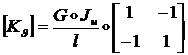(1.2.2.7)
МАТРИЦА ЖЕСТКОСТИ
ИЗГИБА
Для этого случая имеем следующие степени свободы:
- перемещения узлов 1
и 2 вдоль оси ;
- углы поворота
сечений в узлах 1 и 2 относительно оси .
Силовые факторы:
- силы в узлах 1 и 2,
действующие вдоль оси ;
- моменты сил в узлах
1 и 2 относительно оси .
Вектор силовых факторов 
будет связываться с
вектором степеней свободы 
посредством матрицы
жесткости размерности (4х4):
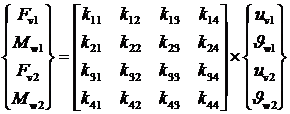(1.2.2.8)
Уравнения
равновесия элемента для изгиба относительно оси имеют вид:
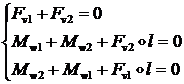(1.2.2.9)
Для нахождения матрицы жесткости нам понадобятся уравнения
изогнутой оси балки. В п. 1.2.1 были получены дифференциальные уравнения
второго порядка для перемещений 
:
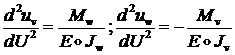(1.2.2.10)
а также дифференциальные уравнения связи углов поворота
сечения 
, с перемещениями :
(1.2.2.11)
В уравнениях (1.2.2.10) внутренние силовые факторы 
являются функциями координаты . Воспользуемся дифференциальными уравнениями равновесия
стержня [8,9]:
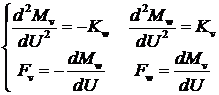(1.2.2.12)
Здесь: 
- внешние силы вдоль
осей и на единицу длины
стержня;
-
"перерезывающие" силы в сечении стержня.
С помощью (1.2.2.12) из уравнений (1.2.2.10) получим следующие дифференциальные уравнения четвертого порядка для изогнутой оси балки:
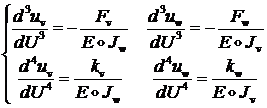(1.2.2.13)
Так как в МКЭ все силовые факторы можно свести к узловым, то можно считать справедливыми условия:
(1.2.2.14)
Тогда общее решение уравнений (1.2.2.13), например, для 
:
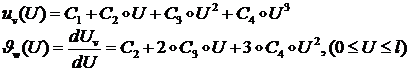(1.2.2.15)
Рассмотрим теперь различные случаи значений степеней свободы.
Случай 1
(рис. 1.2.4 (а))
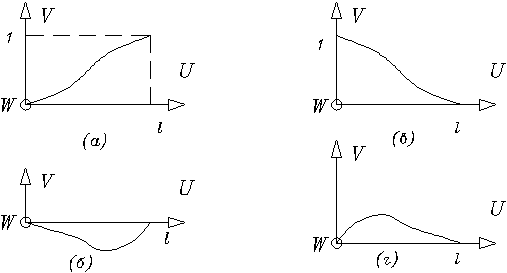
Рис. 1.2.4
Из уравнений (1.2.2.15) для общего решения тогда получим:
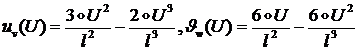(1.2.2.16)
а из уравнений (1.2.2.12) и (1.2.2.13) -
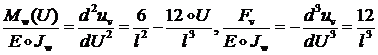(1.2.2.17)
Из (1.2.2.17) следует: 
.
Тогда из уравнений равновесия (1.2.2.9) найдем:
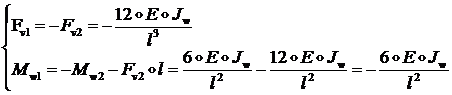(1.2.2.18)
С другой стороны, из (1.2.2.8) следует:
(1.2.2.19)
Отсюда получаем значения из третьего столбца:
(1.2.2.20)
Случай 2
(рис. 1.2.4 (б))
Из уравнений (1.2.2.15) получим:
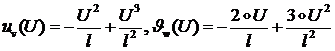(1.2.2.21)
а из (1.2.2.10) и (1.2.2.13):
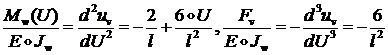(1.2.2.22)
Из (1.2.2.22) следует:
(1.2.2.23)
Тогда из уравнений равновесия (1.2.2.9) найдем:
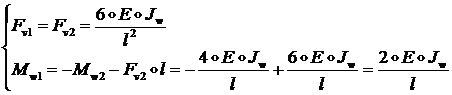(1.2.2.24)
Воспользовавшись уравнениями (1.2.2.8), найдем значения для четвертого столбца:
(1.2.2.25)
Случай 3
(рис. 1.2.4 (в))
Воспользовавшись относительной симметрией деформированных состояний для случаев 1 и 3, сразу найдем:
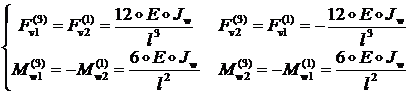(1.2.2.26)
Тогда из (1.2.2.8) получим первый столбец матрицы :
(1.2.2.27)
Случай 4
(рис. 1.2.4 (г))
Воспользовавшись относительной симметрией деформированных состояний для случаев 2 и 4, найдем:
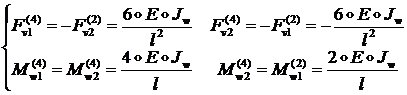(1.2.2.27)
Тогда из (1.2.2.8) найдем второй столбец матрицы :
(1.2.2.28)
Окончательно получим следующий вид матрицы :
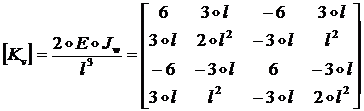(1.2.2.29)
МАТРИЦА ЖЕСТКОСТИ
ИЗГИБА
Степени свободы:
- перемещения узлов 1 и
2 вдоль оси ;
- углы поворота
сечений в узлах 1 и 2 относительно оси .
Силовые факторы:
- силы в узлах 1 и 2,
действующие вдоль оси ;
- моменты сил в узлах
1 и 2 относительно оси .
Изгиб стержня
относительно оси полностью подобен
изгибу стержня относительно оси .
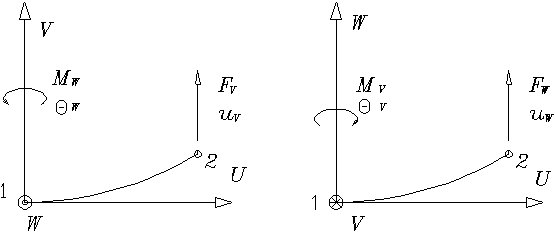
(а) (б)
Рис. 1.2.5
Как видно из рис. 1.2.5 (а) и (б) это подобие может быть достигнуто заменой:
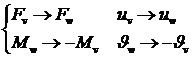(1.2.2.31)
В формулах (1.2.2.31) следует обратить внимание на знак
"-" при переопределении момента сил и угла поворота. С учетом
(1.2.2.31) из формул (1.2.2.30) получим выражение для матрицы :
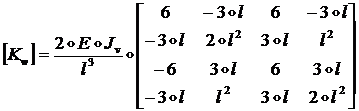(1.2.2.32)