Матрица жесткости
1.2 Одномерные элементы
1.2.1 Балочная теория стержня
Рассмотрим прямой стержень длины ![]() с постоянным сечением
с введенной для него л.с.к.
с постоянным сечением
с введенной для него л.с.к. ![]() (рис. 1.2.1.).
(рис. 1.2.1.).
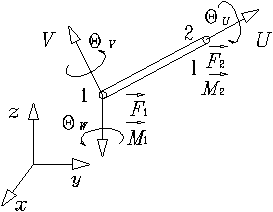
Рис. 1.2.1
Концы стержня обозначены цифрами 1 и 2. Ось ![]() направлена от 1 к 2 и имеет начало в точке стержня 1. Оси
направлена от 1 к 2 и имеет начало в точке стержня 1. Оси ![]() и
и ![]() являются главными
осями стержня. На рис. 1.2.1 показаны положительные направления поворотов, а
также действия моментов сил, вокруг осей
являются главными
осями стержня. На рис. 1.2.1 показаны положительные направления поворотов, а
также действия моментов сил, вокруг осей ![]() ; вектора сил
; вектора сил ![]() и
и ![]() и моментов
и моментов ![]() и
и ![]() могут быть приложены к
концам стержня 1 и 2 соответственно.
могут быть приложены к
концам стержня 1 и 2 соответственно.
Рассмотрим сечение стержня (рис. 1.2.2); ось ![]() на рисунке направлена
на нас.
на рисунке направлена
на нас.
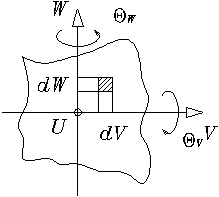
Рис. 1.2.2
Здесь же выделена элементарная площадь сечения стержня: ![]() . Дальше для определенности будем считать, что конец стержня
1 заделан (т.е.
. Дальше для определенности будем считать, что конец стержня
1 заделан (т.е. ![]() , где
, где ![]() - угол поворота сечения 1, а
- угол поворота сечения 1, а ![]() - перемещение конца
1), а конец 2 свободен и к нему в общем случае приложены сила
- перемещение конца
1), а конец 2 свободен и к нему в общем случае приложены сила ![]() и момент сил
и момент сил ![]() .
.
Для малых деформаций стержня будет справедлив принцип суперпозиции действия силовых факторов, т.е. полная деформация стержня будет являться суперпозицией деформаций, каждая из которых вызвана одним из шести приложенных силовых факторов.
При этом сила ![]() будет растягивать (или
сжимать) стержень вдоль оси
будет растягивать (или
сжимать) стержень вдоль оси ![]() ; сила
; сила ![]() и момент
и момент ![]() будут изгибать
стержень относительно оси
будут изгибать
стержень относительно оси ![]() , сила
, сила ![]() и момент
и момент ![]() будут изгибать
стержень относительно оси
будут изгибать
стержень относительно оси ![]() , а момент
, а момент ![]() будет закручивать
стержень относительно оси
будет закручивать
стержень относительно оси ![]() .
.
Рассмотрим сначала действие растягивающей силы ![]() . Разумно предположить, что при этом единственной отличной от
нуля компонентой тензора напряжений будет
. Разумно предположить, что при этом единственной отличной от
нуля компонентой тензора напряжений будет ![]() . Пользуясь тогда формулами (1.1.1.6) для связи компонент
вектора напряжений
. Пользуясь тогда формулами (1.1.1.6) для связи компонент
вектора напряжений ![]() и вектора деформации
и вектора деформации ![]() , найдем:
, найдем:
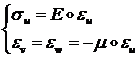 (1.2.1.1)
(1.2.1.1)
Видно, что стержень будет сжиматься в сечении одновременно с
его растяжением вдоль оси ![]() . Перемещение конца 2 вдоль оси
. Перемещение конца 2 вдоль оси ![]() равно:
равно:
![]()
Напряжение ![]() можно считать
постоянным и равным:
можно считать
постоянным и равным:
![]()
где: ![]() - площадь сечения стержня.
- площадь сечения стержня.
Окончательно мы находим следующее соотношение между
перемещением ![]() и силой
и силой ![]() вдоль оси
вдоль оси ![]() :
:
![]() (1.2.1.2)
(1.2.1.2)
Получена первая важная формула теории сопротивления материалов (сопромат) является самой простой. Условие малости деформаций здесь:
![]()
Перейдем теперь к рассмотрению кручения стержня вокруг оси ![]() под воздействием
момента сил
под воздействием
момента сил ![]() , приложенного на конце 2. Сначала рассмотрим частный случай
круглого сечения стержня (рис. 1.2.3) радиуса
, приложенного на конце 2. Сначала рассмотрим частный случай
круглого сечения стержня (рис. 1.2.3) радиуса ![]() .
.
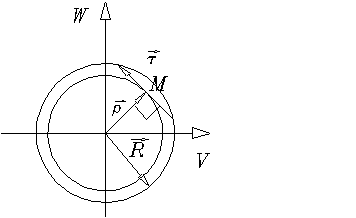
Рис. 1.2.3
Из условий симметрии задачи кручения стержня кругового
сечения деформация такого стержня будет заключаться в том, что каждое (круглое) сечение стержня в
результате повернется как целое на некоторый угол ![]() . Введем угол кручения
. Введем угол кручения ![]() как угол поворота
сечения, отнесенный к единице длины стержня, т.е.:
как угол поворота
сечения, отнесенный к единице длины стержня, т.е.:
![]() (1.2.1.3)
(1.2.1.3)
Из условия приложения крутящего момента и постоянства
сечения стержня вдоль его оси ![]() ясно, что угол
кручения
ясно, что угол
кручения ![]() должен быть
постоянной, независящей от
должен быть
постоянной, независящей от ![]() , величиной:
, величиной: ![]()
Тогда максимальный угол поворота сечения 2 равен:
![]()
а максимальные перемещения точек сечения:
![]()
Условие малости деформаций означает что:
![]() (1.2.1.4)
(1.2.1.4)
Последнее и есть условие справедливости принципа суперпозиции для кручения.
Так как сечение с координатой ![]() повернуто на угол:
повернуто на угол:
![]()
то перемещения точек сечения вдоль оси ![]() и
и ![]() равны:
равны:
![]() (1.2.1.5)
(1.2.1.5)
а перемещения вдоль оси ![]() :
: ![]()
Тогда компоненты вектора деформаций ![]() :
:
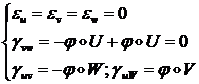 (1.2.1.6)
(1.2.1.6)
С помощью формул (1.1.1.6) получим компоненты ![]() :
:
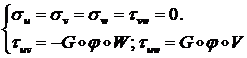 (1.2.1.7)
(1.2.1.7)
где: 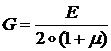 - модуль сдвига.
- модуль сдвига.
Из формул (1.2.1.7) следует, что единственными отличными от
нуля компонентами вектора напряжений ![]() являются касательные,
сдвиговые компоненты
являются касательные,
сдвиговые компоненты ![]() .
.
При этом проекции ![]() сдвигового напряжения
сдвигового напряжения ![]() таковы, что полное
сдвиговое напряжение
таковы, что полное
сдвиговое напряжение ![]() в произвольной точке
в произвольной точке ![]() круглого сечения
направлено по касательной к окружности, проведенной из центра сечения через эту
точку, а величина напряжений
круглого сечения
направлено по касательной к окружности, проведенной из центра сечения через эту
точку, а величина напряжений ![]() равна (рис. 1.2.3):
равна (рис. 1.2.3):
![]() (1.2.1.8)
(1.2.1.8)
где ![]() - радиус текущей
окружности (
- радиус текущей
окружности (![]() ).
).
Элементарная внутренняя сила ![]() , закручивающая стержень, равна:
, закручивающая стержень, равна:
![]()
а соответствующий элементарный момент ![]() равен:
равен: ![]() , так как вектор
, так как вектор ![]() перпендикулярен к
вектору
перпендикулярен к
вектору ![]() .
.
Так как полный момент внутренних сил в каждом сечении равен
приложенному моменту ![]() , то получим формулу связи момента
, то получим формулу связи момента ![]() с напряжениями
с напряжениями ![]() :
:
![]() (1.2.1.9)
(1.2.1.9)
а с учетом формулы (1.2.1.8):
![]() (1.2.1.10)
(1.2.1.10)
Стоящий здесь интеграл называют полярным моментом сечения и
обозначают ![]() :
:
![]() (1.2.1.11)
(1.2.1.11)
В результате мы получили следующую формулу связи угла ![]() для конца 2 с
крутящими моментами
для конца 2 с
крутящими моментами ![]() [9]:
[9]:
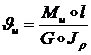 (1.2.1.12)
(1.2.1.12)
В случае же произвольного сечения стержня задача кручения
очень усложняется тем, что сечение начинает вместе с поворотом вокруг оси ![]() испытывать перемещение
точек из плоскости сечения, т.е. сечение перестает быть плоским. Существует
общая теория кручения таких стержней
[8]. В ней вводится понятие крутильной жесткости сечения
испытывать перемещение
точек из плоскости сечения, т.е. сечение перестает быть плоским. Существует
общая теория кручения таких стержней
[8]. В ней вводится понятие крутильной жесткости сечения ![]() , которая связывает угол кручения
, которая связывает угол кручения ![]() с крутящим моментом
с крутящим моментом ![]() :
:
![]()
так что в общем случае угол поворота сечения 2 - ![]() равен:
равен:
![]() (1.2.1.13)
(1.2.1.13)
Теория позволяет аналитически находить ![]() для любого сечения. В
сопромате вводится понятие обобщенного момента кручения
для любого сечения. В
сопромате вводится понятие обобщенного момента кручения ![]() по аналогии с полярным
моментом
по аналогии с полярным
моментом ![]() :
:
![]()
Тогда формула (1.2.1.13) приобретает вид, аналогичный (1.2.1.12)
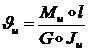 (1.2.1.14)
(1.2.1.14)
Значение ![]() для некоторых
стандартных сечений приведены в [9].
для некоторых
стандартных сечений приведены в [9].
Перейдем теперь к наиболее сложному вопросу изгиба стержней. Балочная теория стержня утверждает справедливость для слабых деформаций так называемой гипотезы плоских сечений [9].
Согласно этой гипотезе, сечение стержня при изгибе остается
плоским, поворачиваясь в пространстве как жесткое целое вокруг осей ![]() и
и ![]() . Отсюда легко находим
перемещение точек сечения стержня вдоль оси
. Отсюда легко находим
перемещение точек сечения стержня вдоль оси ![]() , т.е. из плоскости сечения (
, т.е. из плоскости сечения (![]() ):
):
![]() (1.2.1.15)
(1.2.1.15)
Остальные перемещения можно считать равными нулю: ![]()
Тогда отличные от нуля компоненты вектора деформаций ![]() :
:
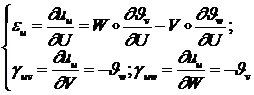 (1.2.1.16)
(1.2.1.16)
В балочной теории мы пренебрегаем деформациями сдвига,
считая основной продольную деформацию ![]() , меняющуюся по линейному закону в пределах сечения.
, меняющуюся по линейному закону в пределах сечения.
Соответствующее нормальное внутреннее напряжение ![]() равно:
равно:
![]() (1.2.1.17)
(1.2.1.17)
Растягивающая сила ![]() и изгибающие моменты
внутренних напряжений
и изгибающие моменты
внутренних напряжений ![]() относительно осей
относительно осей ![]() и
и ![]() равны соответственно:
равны соответственно:
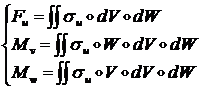 (1.2.1.18)
(1.2.1.18)
Если воспользоваться (1.2.1.17), то формулы (1.2.1.18) примут вид:
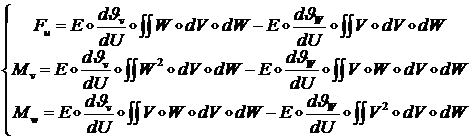
(1.2.1.19)
Так как сейчас мы не рассматриваем растяжение стержня, то
можем считать: ![]() Тогда в силу произвольности
значений производных
Тогда в силу произвольности
значений производных ![]() из (1.2.1.19) для
из (1.2.1.19) для ![]() следует:
следует:
![]() (1.2.1.20)
(1.2.1.20)
Условие (1.2.1.20) показывает, что начало координат ![]() ,
лежит в центре тяжести сечения. Поэтому ось стержня представляется
совокупностью центров тяжести всех
сечений стержня. В системе координат с началом в центре тяжести сечения с
помощью поворота осей
,
лежит в центре тяжести сечения. Поэтому ось стержня представляется
совокупностью центров тяжести всех
сечений стержня. В системе координат с началом в центре тяжести сечения с
помощью поворота осей ![]() ,
, ![]() в плоскости сечения
можно добиться того, чтобы:
в плоскости сечения
можно добиться того, чтобы:
![]() (1.2.1.21)
(1.2.1.21)
Тогда формулы для изгибающих моментов принимают известный вид [9]:
![]() (1.2.1.22)
(1.2.1.22)
где: ![]() - момент инерции сечения
относительно оси
- момент инерции сечения
относительно оси ![]() ;
;
![]() - момент инерции
сечения относительно оси
- момент инерции
сечения относительно оси ![]() .
.
В этом случае оси ![]() и
и ![]() называют главными
осями сечения стержня.
называют главными
осями сечения стержня.
Пусть теперь: ![]() - перемещения точек
оси стержня вдоль осей
- перемещения точек
оси стержня вдоль осей ![]() и
и ![]() соответственно в
результате его изгиба. Эти перемещения легко могут быть связаны с углами
поворота сечения около осей
соответственно в
результате его изгиба. Эти перемещения легко могут быть связаны с углами
поворота сечения около осей ![]() на основе гипотезы,
что касательный вектор
на основе гипотезы,
что касательный вектор ![]() к оси деформированного
стержня остается в результате деформации нормальным к плоскости сечения стержня
(именно эта гипотеза отражает принятое в балочной теории положение о том, что
деформации сдвига равны нулю:
к оси деформированного
стержня остается в результате деформации нормальным к плоскости сечения стержня
(именно эта гипотеза отражает принятое в балочной теории положение о том, что
деформации сдвига равны нулю: ![]() ):
):
![]() (1.2.1.23)
(1.2.1.23)
С помощью формул (1.2.1.22) и (1.2.1.23) получаем известные дифференциальные уравнения изогнутой оси балки:
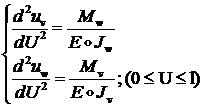 (1.2.1.24)
(1.2.1.24)
В случае заделки на конце l граничными условиями для уравнений (1.2.1.24) будут:
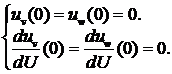 (1.2.1.25)
(1.2.1.25)
Формулы (1.2.1.24) и (1.2.1.25) определяют уравнения
изогнутой оси балки. Рассмотрим два случая: действие на конце 2 моментов ![]() и действие на конце 2
сил
и действие на конце 2
сил ![]() .
.
В первом случае внутренние силовые факторы ![]() равны приложенным моментам
на конце стержня 2.
равны приложенным моментам
на конце стержня 2.
Для ![]() тогда имеем:
тогда имеем:
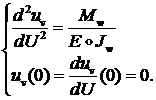
откуда: 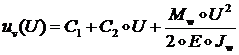
Из граничных условий следует: ![]()
Окончательно перемещение ![]() и угол поворота
и угол поворота ![]() равны:
равны:
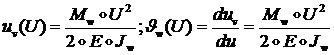
Для перемещений конца стержня 2 тогда получим [9]:
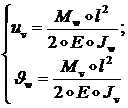 (1.2.1.26)
(1.2.1.26)
аналогично:
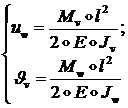 (1.2.1.27)
(1.2.1.27)
Во втором случае силовые факторы ![]() меняются вдоль оси
стержня по формулам:
меняются вдоль оси
стержня по формулам:
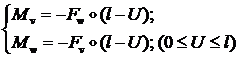 (1.2.1.28)
(1.2.1.28)
Для ![]() тогда получим:
тогда получим:
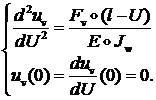
Общее решение имеет вид: 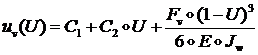
Из граничных условий следует система уравнений:
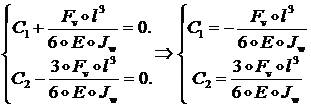
откуда: 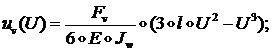
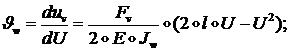
Для перемещений ![]() и угла поворота
и угла поворота ![]() конца стержня 2
получим [9]:
конца стержня 2
получим [9]:
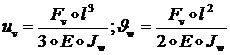 (1.2.1.29)
(1.2.1.29)
аналогично:
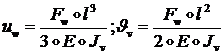 (1.2.1.30)
(1.2.1.30)
Полученные в п. 1.2.1 уравнения балочной теории стержня будут применены в п. 1.2.2 для построения конечного элемента стержня.