1.1.8 Уравнения связи. Конденсация

Рассмотрим конечно-элементную модель с узлами. С каждым узлом , связано определенное число степеней свободы , определяемое типом конечных элементов, имеющих общим узел (например, для мембраны ). Поэтому общее число степеней свободы конечно-элементной сетки равно сумме по всем узлам:

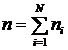
Зная вектор силовых факторов в узлах конечно-элементной сетки, и составив глобальную матрицу жесткости , можно определить вектор степеней свободы , решая уравнения равновесия конструкции (см. п. 1.1.5):

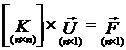(1.1.8.1)

Как правило, задача статики ставится для закрепленной конструкции, т.е. некоторые перемещения (углы поворота) равны нулю (закреплены). Задание нулевых перемещений (углов поворота) - стандартные граничные условия (см. [ИСПА]). Кроме стандартных граничных условий в [ИСПА] есть возможность задавать особые граничные условия, в которых некоторые степени свободы связаны так называемыми уравнениями связи.

Так как в главе 1 рассматриваются только линейные задачи механики, то общий вид уравнений связи для случая, когда число связей в системе с степенями свободы равно , следующий:

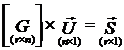(1.1.8.2)

т.е. уравнения связи представляют собой систему линейных алгебраических уравнений относительно вектора степеней свободы системы .

Вектор - правая часть.

Поэтому из степеней свободы системы можно с помощью уравнений связи (1.1.8.2) исключить степеней свободы. В результате получим новые уравнения равновесия конструкции

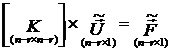(1.1.8.3)

с размерностью (числом степеней свободы) .

Метод снижения размерности системы уравнений при помощи исключения некоторых степеней свободы называется конденсацией [3]. Для проведения конденсации выделим в векторе степеней свободы системы с размерностью вектор исключаемых степеней свободы (с размерностью )) и вектор сохраняемых степеней свободы (с размерностью ).

Уравнения равновесия конструкции (1.1.8.1) в этом случае можно записать в следующем виде:

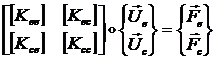(1.1.8.4)

Как правило, выбор исключаемых степеней свободы произволен, хотя возникают особые случаи, когда это неверно [3].

Уравнения связи (1.1.8.2) представим в виде:

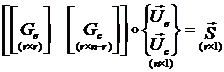(1.1.8.5)

Из уравнений (1.1.8.5) выразим исключаемый вектор :

(1.1.8.6)

Вектор можно тогда выразить через :

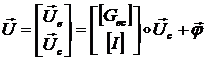
или

(1.1.8.7)

Здесь введены следующие обозначения:

- единичная матрица размерности ;

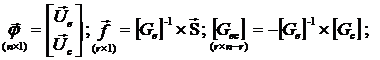
Матрица преобразования равна:

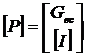(1.1.8.8)

Уравнения (1.1.8.7) можно рассматривать как уравнения преобразования координат с переходом от "старых" координат "новым" - . Поэтому уравнения равновесия конструкции в "новых" координатах можно получить, если найдены преобразования для матрицы жесткости и вектора силовых факторов . Решим эту задачу, используя потенциал системы (см. п. 1.1.1). До конденсации:

(1.1.8.9)

После конденсации имеем (см. (1.1.8.7)): , поэтому потенциал будет функцией от вектора :

После простых преобразований найдем:

(1.1.8.10)

После варьирования найдем новые уравнения равновесия:

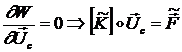(1.1.8.11)

Здесь введены преобразованная матрица жесткости размерности и преобразованная правая часть размерности :

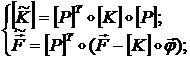(1.1.8.12)

Таким образом, процедура конденсации системы уравнений проведена и получены конденсированные уравнения равновесия конструкции.