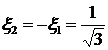1.1.6. Численное интегрирование в МКЭ
При нахождении матрицы жесткости элемента или узловых сил мы сталкиваемся с необходимостью вычислять интегралы вида:
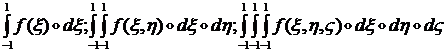
В силу сложности подынтегральных функций в общем случае взять эти интегралы аналитически не удается. Поэтому для их нахождения в МКЭ используют численные методы интегрирования. Рассмотрим сначала самый простой случай одномерного интеграла:
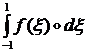 (1.1.6.1)
(1.1.6.1)
В численных методах интегрирования интеграл (1.1.6.1) заменяется приближенно на сумму:
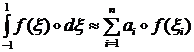 (1.1.6.2)
(1.1.6.2)
где: ![]() - выбранные точки
интегрирования
- выбранные точки
интегрирования ![]()
![]() - весовые коэффициенты.
- весовые коэффициенты.
Различные численные методы предлагают так или иначе определять
![]() и
и ![]() , но все они сходятся в том, что при
, но все они сходятся в том, что при ![]() выполняется предельное
условие:
выполняется предельное
условие:
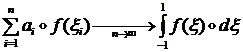 (1.1.6.3)
(1.1.6.3)
Так как вычисления подынтегральной функции, например, для матрицы жесткости, является весьма трудоемкой задачей, в МКЭ наиболее желательны такие численные методы, которые обеспечивали бы наибольшую точность при наименьшем числе точек интегрирования. В этом смысле очень хорошим является метод Гаусса [6].
В методе Гаусса величины ![]() и
и ![]() выбираются таким образом,
чтобы формула (1.1.6.2) представляла собой
точное равенство для функции
выбираются таким образом,
чтобы формула (1.1.6.2) представляла собой
точное равенство для функции ![]() . Так как число варьируемых величин в методе Гаусса равно
. Так как число варьируемых величин в методе Гаусса равно ![]() , где
, где ![]() - число точек интегрирования,
то максимальный порядок интегрирования:
- число точек интегрирования,
то максимальный порядок интегрирования: ![]() . Тогда
. Тогда ![]() величин
величин ![]() и
и ![]() будут определены в
результате решения системы
будут определены в
результате решения системы ![]() алгебраических
уравнений.
алгебраических
уравнений.
Рассмотрим примеры:
1) ![]() = 1,
= 1, ![]() = 1
= 1
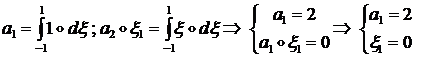
2) ![]() = 2 ,
= 2 , ![]() = 3
= 3
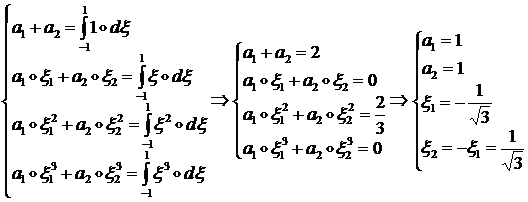
В таблице 1.1.1 приведены результаты расчетов для ![]() .
.
Таблица 1.1.1
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
Рассмотрим теперь двумерный интеграл:
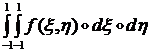 (1.1.6.4)
(1.1.6.4)
Производя в интеграле (1.1.6.4) сначала интегрирование по ![]() , получим с помощью (1.1.6.2):
, получим с помощью (1.1.6.2):
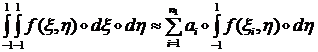 (1.1.6.5)
(1.1.6.5)
где: ![]() - число точек Гаусса в направлении
- число точек Гаусса в направлении ![]() .
.
Численно интегрируя оставшиеся одномерные интегралы, получим из (1.1.6.5):
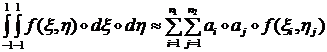 (1.1.6.6)
(1.1.6.6)
где: ![]() - число точек Гаусса в
направлении
- число точек Гаусса в
направлении ![]() .
.
Аналогично для тройного интеграла:
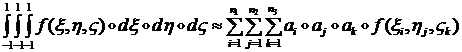 (1.1.6.7)
(1.1.6.7)
где: ![]() - число точек Гаусса в направлениях
- число точек Гаусса в направлениях ![]() соответственно.
соответственно.
Очень важным является вопрос о выборе числа точек интегрирования. Максимально допустимый порядок интегрирования в трехмерном случае определяется требованием, чтобы интеграл:
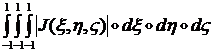 (1.1.6.8)
(1.1.6.8)
представляющий собой объем элемента, вычислялся бы точно.
В противном случае даже при сгущении конечно-элементной сетки не будет сходимости конечно-элементного решения к точному вследствие неверного вычисления объема.
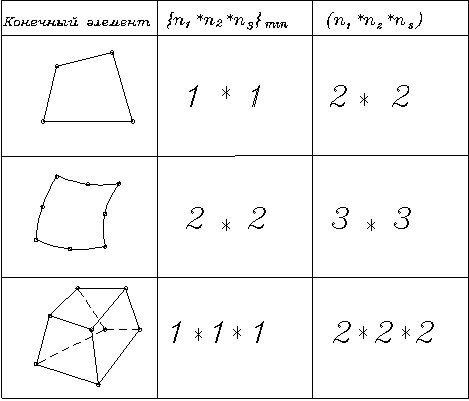
В таблице 1.1.2 приведены
минимально допустимые ![]() и рекомендуемые
и рекомендуемые ![]() числа точек Гаусса для
некоторых, рассмотренных в главе 1 элементов.
числа точек Гаусса для
некоторых, рассмотренных в главе 1 элементов.
Таблица 1.1.6