1.1.4. Матрица жесткости элемента. Уравнение равнове­сия элемента

 

Рассмотрим для общности трехмерную модель тела. Пусть мы провели дискретизацию тела на трехмерные конечные элементы. В пределах каждого конечного элемента, в соответствии с п. 1.1.3., искомое поле перемещений :

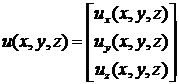
аппроксимируется по своим значениям  в узлах элемента с помощью функций формы элемента :

       (1.1.4.1)

Тогда вектор деформации , определяемый через перемещения по формуле (1.1.1.4), будет иметь следующую  аппроксимацию (см. п. 1.1.1):

(1.1.4.2)

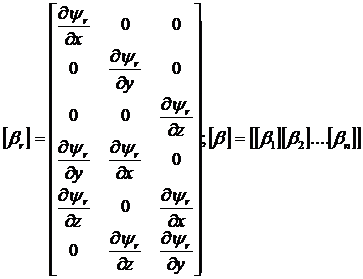
Здесь:  - вектор степеней свободы элемента (3xn компонент);

 - матрица деформирования элемента.

Итак, согласно (1.1.4.2), вектор деформации аппроксимируется в пределах конечного элемента с помощью матрицы деформирования  и вектора степеней свободы элемента .

Как мы знаем из п. 1.1.1, энергия деформации упругого тела  определяется формулой (1.1.1.10):

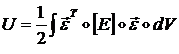              (1.1.4.3)

где:  - 6-и компонентный вектор деформации (1.1.1.4);

 - матрица упругости однородной изотропной среды.

Интегрирование ведется по объему тела.

Тогда в силу аддитивности интеграла энергия деформации тела  равна сумме энергий деформации элементов , на которые разбито тело:

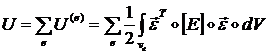         (1.1.4.4)

С помощью (1.1.4.2) получим :

        (1.1.4.5)

где:  - матрица жесткости элемента.

Матрица жесткости элемента является важнейшим понятием в приложении МКЭ в механике.

Так как полученная здесь формула для матрицы жесткости является общей, выпишем ее еще раз:

       (1.1.4.6)

Матрица жесткости  имеет размерность , где  - число степеней свободы конечного элемента.

Матрица  - есть матрица деформирования элемента.

Собственно говоря, конечный элемент можно считать построенным, если построена его матрица жесткости.

Пусть:  - силы, действующие в узлах конечного элемента.

Тогда работа этих сил на узловых перемещениях, в соответствии с определением работы в механике, равна:

     (1.1.4.7)

где:

Как следует из принципа Лагранжа, конечный элемент  будет  характеризоваться потенциалом :

                      (1.1.4.8)

С помощью (1.1.4.5) и (1.1.4.7) получим:

                                                         (1.1.4.9)

Видим что  - есть просто функция от , так что первая вариация  будет просто равна дифференциалу

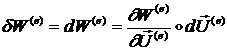
В соответствии с принципом Лагранжа первая вариация , а значит и дифференциал  равны нулю.

Но равенство нулю дифференциала функции возможно тогда, когда равны нулю все ее первые производные, т.е. уравнение Лагранжа для МКЭ в механике примет вид:

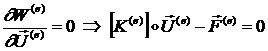                                                       (1.1.4.10)

В результате мы получили уравнения равновесия конечного элемента, представляющие собой систему неоднородных линейных алгебраических уравнений относительно неизвестного вектора степеней свободы элемента :

                    (1.1.4.11)

Итак, мы нашли, что узловые силы    и узловые перемещения  конечного элемента связаны между собой с помощью матрицы жесткости элемента .

Этим и определяется особое значение матрицы жесткости конечного элемента.

Заметим, что из формулы (1.1.4.6), определяющей матрицу жесткости элемента, следует ее симметричность:

  (для любой пары индексов   и ).

Кроме того, так как энергия деформации элемента  всегда положительна и равна нулю только при отсутствии деформаций, то из (1.1.4.5) следует, что матрица жесткости элемента  положительно определенная.

Этими двумя свойствами исчерпываются основные свойства матрицы жесткости элемента.