1.1.3. Основные положения МКЭ

 

Рассмотрим тело, нагруженное произвольным образом. В результате действия приложенных сил тело как-то деформируется, и эта деформация может быть описана с помощью поля перемещений: , согласно п. 1.1.1. Найти равновесное поле перемещений  - вот задача теории упругости. Метод конечных элементов (МКЭ) позволяет приближенно найти поле перемещений упругого тела. Основная идея МКЭ состоит в том, что тело разбивается на совокупность достаточно малых подобластей, называемых в дальнейшем конечными элементами. Эта процедура называется дискре­тизацией тела. В пределах каждого конечного элемента поле перемещений аппрок­сими­руется с помощью так называемых функций формы по известным значениям перемещений ,  ( - число узлов конечного элемента) в узлах элемента. В целях иллюстрировать эту идею на рис. 1.1.4 изображена  плоская  треугольная область, разбитая на конечные элементы треугольной формы с узлами в вершинах треугольников.

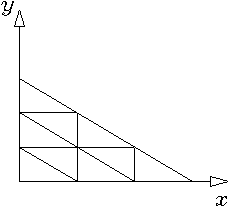
Рис. 1.1.4

 

Заметим, что материал данного п. 1.1.3 справедлив не только для МКЭ в механике, но и для других областей применения МКЭ, например, для задач теплопроводности твердых тел, где вместо поля перемещений в качестве основной неизвестной величины служит поле температур: .

С помощью функций формы аппроксимируются как геометрия конечного элемента, так и поля неизвестных величин, например поле перемещений . В общем случае функции формы, употребляемые для аппроксимации геометрии, отличаются от функций форм, использующихся для аппроксимации полей неизвестных величин.

 

ОПРЕДЕЛЕНИЕ

 

Конечным элементом будем называть некоторую малую область тела в сово­куп­ности с заданными в ней функциями формы, аппроксимирующими геометрию конечного элемента и заданные на нем неизвестные величины.

 

Для описания конечного элемента необходимо ввести систему координат. Упот­ребляемые в системе ИСПА системы координат являются правыми декартовыми и описаны в [ИСПА]. Из этих систем координат мы будем рассматривать две:

1) глобальная декартовая система координат ;

2) локальная система координат конечного элемента .

 

Если  первая система координат существует всегда, то последняя определяется только для элементов стержней и двумерных элементов.

На рис. 1.1.5 показан пример выбора локальных  систем  координат для элемента стержня и треугольного элемента.

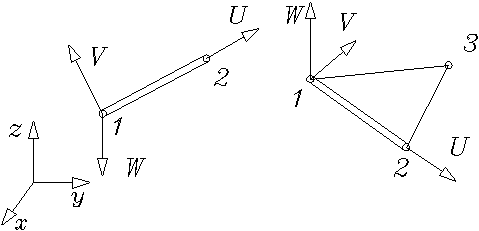
Рис. 1.1.5

 

Цифрами обозначены номера узлов элементов.

Ось  направлена от узла 1 к узлу 2 и имеет  начало в узле 1. Для стержня оси  и  являются  главными осями. Понятие главных осей будет введено в разделе 1.2. Для двухмерных  элементов  ось   направлена в положительное полупространство оси , а ось    находится в плоскости расположения элемента и направлена в соответствии с тем фактом, что  - правая система координат [ИСПА].

 

Перейдем теперь к более подробному рассмотрению аппроксимации неизвестных величин. Например, для плоской задачи (рис. 1.4) в качестве неизвестной величины вы­ступает 2-х компонентное поле перемещений , которое мы будем записывать или в виде  вектора-столбца:

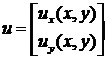
или в виде транспонированного вектора-строки: .

В каждом узле конечного элемента (на рис. 1.1.4 конечные элементы - треугольные с узлами в вершинах) перемещения в МКЭ считаются неизвестными и определяются так называемым вектором степеней свободы узла, обозначаемым :

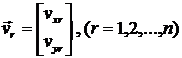
где:  - число узлов конечного элемента. Компоненты  называются степенями свободы узла.

Вместе с векторами , в МКЭ  вводится  вектор степеней свободы всего элемента :

 

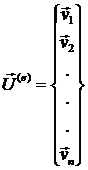
В нашем случае число степеней свободы конечного элемента равно 2xn.

Искомое поле перемещений в МКЭ аппроксимируется тогда  следующим образом:

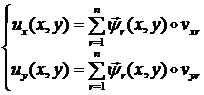
или в векторной форме:

             (1.1.3.1)

Здесь:  - функция формы конечного элемента, относящаяся к узлу .

Основное свойство функций формы состоит в том, что  в узле  и  в узле , (= 1, 2, ... , ).

Из этого свойства сразу же следует что:

         (1.1.3.2)

т.е. в узлах элемента аппроксимированное с помощью (1.1.3.1) поле перемещений  действительно совпадает со своими значениями в узлах элемента .

В МКЭ принято в качестве функций формы  использовать полиномы. Указан­ное основное свойство функций форм позволяет однозначно определять вид полинома.

Более подробно этот вопрос будет рассмотрен дальше в  приложениях МКЭ.

В результате вместо необходимости определять непрерывную величину , имеющую бесконечное число степеней свободы, в МКЭ требуется определить конечное число неизвестных, являющихся степенями свободы системы в узлах конечно-элементной сетки.

Это осуществляется путем решения алгебраической системы уравнений, являющей­ся уравнениями Лагранжа для вариационного принципа, который может быть построен не только в механике, но и в других задачах.

Введем понятие совместности двух конечных элементов. Два конечных элемента будем называть совместными, если в механике - поле перемещений  (в задачах теплопроводности - поле температур ) не терпит разрыва на общей границе этих элементов.

Таким образом, если все элементы конечно-элементной сетки являются совместны­ми, то поле перемещений  (поле температур ) будет непрерывным во всей области решаемой задачи. Совместность элементов имеет также тесную связь со сходимостью решения конечно-элементной задачи к точному при сгущении конечно-элементной сетки (см. п. 1.1.7).

Перейдем теперь к изложению МКЭ в механике.