1.1.2 Одномерные, двумерные и трехмерные модели упругих тел

Полученные в п.1.1.1. результаты справедливы для произвольного упругого тела и определяют общую трехмерную модель. Но существуют особые случаи, когда вместо трехмерной модели тела более удобно рассматривать одномерную или двумерную модели.

Именно, если протяженность тела в двух его направлениях много меньше протяженности в третьем направлении, то такое тело, называемое дальше стержнем, удобно представлять одномерной моделью. В одномерной модели (стержень) все основные величины, определяемые в теории упругости (перемещения, тензор деформаций, тензор напряжений и др.), зависят только от одной переменной, меняющейся вдоль стержня.

На рис. 1.1.3(а) стержень представлен в виде криволинейной линии, представляющей собой ось реального тела. Под сечением стержня в данной точке оси стержня будем понимать сечение тела плоскостью, нормальной к оси стержня в данной точке. Площадь сечения вдоль оси стержня может быть переменной величиной.

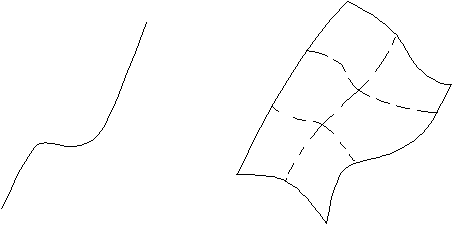
а) b)

Рис. 1.1.3

Особое внимание в дальнейшем мы обратим на случай прямого стержня постоянного сечения, так как в теории сопротивления материалов (сопромат) детально развита теория такого стержня. Это так называемая балочная теория [9].

Виды напряженного состояния такого стержня, как и сама балочная теория, будут рассмотрены в разделе 1.2, посвященном одномерным элементам.

Другой случай имеет место, когда тело в одном направлении имеет гораздо меньшую протяженность, чем в двух остальных. Для такого тела имеет смысл рассматривать двумерную модель, называемую в дальнейшем оболочкой.

На рис. 1.1.3 (б) представлена произвольной формы оболочка в виде неплоской поверхности, представляющей собой срединную (т.е. равноудаленную от "нижней" и "верхней" поверхностей) поверхность оболочки. Для оболочки естественным образом определяется ее толщина, как ее протяженность вдоль направления, нормального к поверхности оболочки в данной точке.

Мы будем рассматривать оболочки постоянной толщины.

В случае плоской оболочки можно различать три типа напряженного состояния, называемые в дальнейшем: "мембрана", "пластина" и "оболочка". Подробно о мембране, пластине и оболочке будет говориться в разделе 1.3, посвященном двумерным элементам.

Раздел 1.4 посвящен трехмерным моделям.