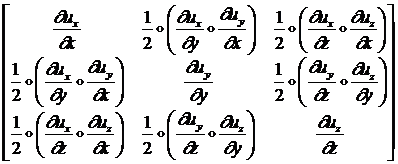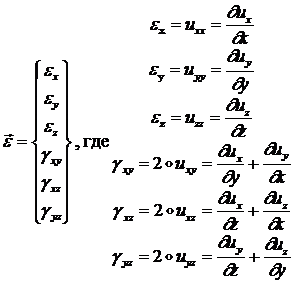ГЛАВА 1

Механика. Статика

 

1.1. Теоретические основы

 

1.1.1. Элементы теории упругости

 

Механика твердых тел, рассматриваемых как сплошные упругие среды, составляет содержание теории упругости.

Подробно эта теория излагается, например, в книгах [7]-[8].

Введем важные в теории упругости понятия: перемещения  точек, деформации и напряжения твердого тела как сплошной среды. Каждую точку тела будем описывать вектором  в декартовой системе координат : . Под воздействием приложенных внешних сил твердое тело, вообще говоря, как-то деформируется, так что новое положение той же точки тела будет описываться новым вектором: . Будем называть вектором перемещения вектор , равный:

                                 (1.1.1.1)

В результате в деформированном теле возникает поле вектора перемещения:  - область пространства, занимаемая телом), но описывать де­фор­мацию тела полем  не совсем удобно, так как при параллельном переносе или повороте тела как  твердого целого  в  нем не возникает никаких деформаций, в то время как поле .

Деформация тела должна описывать  изменения  расстояний  между точками тела.

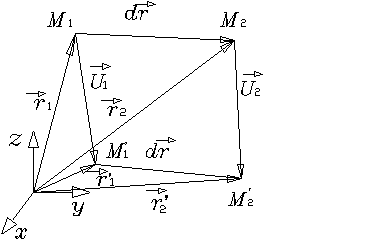
Рис. 1.1.1

На рис.1.1.1 показаны две бесконечно близкие точки тела до деформации: точка , описываемая вектором  и точка , описываемая вектором . В результате деформирования тела первая точка заняла новое положение т.  с вектором , а вторая т.  с вектором , так что вектора перемещений равны для точки :

а для точки :

.

До деформации расстояние между двумя точками  и  описывалось беско­неч­но малым вектором: ,

а после деформации - вектором: .

Вектора  и  также приведены на рис. 1.1.1 и выписанные здесь формулы легко следуют из этого рисунка на основе алгебры векторов. Очевидно, что расстояние  между точками  и  до деформирования тела равно длине вектора , а расстояние  между этими же точками после деформации - длине вектора . Известно, что длина вектора , имеющего в декартовой системе координат  проекции - , равна:

Поэтому: , а

Отсюда следует, что

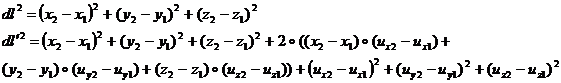
Учитывая выражение для  и тот факт, что в силу бесконечной близости точек  и  справедливы равенства:

 

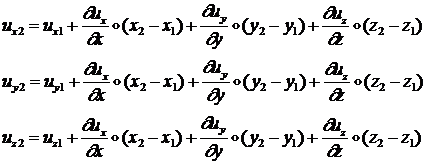
получим следующую формулу для :

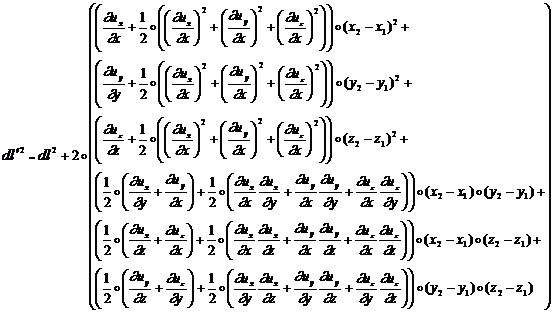 (1.1.1.2)

 

В  широком классе задач технической механики деформации тела оказываются малыми, т.е.:

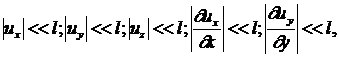 и т.д.

 

где характерный размер задачи.

 

Поэтому мы можем пренебречь в (1.1.1.2) квадратичными по производным от перемещений членам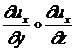и вроде  по сравнению с линейными членами вроде . Тогда формула (1.1.1.2) примет вид:

 

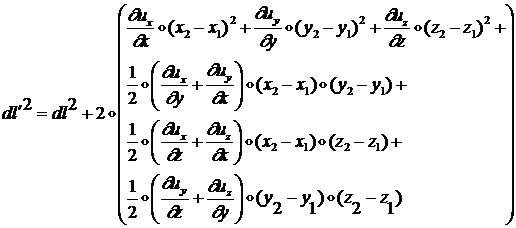
Видим, что изменение расстояния между двумя бесконечно близкими точками упру­гого тела в результате его деформации однозначно определяется первыми производными от перемещений по координатам, а также расстоянием между точками до деформации.

Указанные первые производные от перемещений по координатам принято в теории упругости записывать в виде симметричной матрицы (3x3):

 

компоненты, которой называются тензором деформации и обозначаются:  .

Нетрудно видеть, что компоненты тензора деформации могут быть записаны в ви­де:

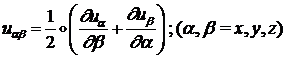                                                        (1.1.1.3)

Очевидно, что тензор деформации  является симметричным, т.е. для любой пары индексов () справедливо:

Кроме того, тензор деформации  является тензором второго ранга, т.к. характе­ризуется двумя индексами.

Симметричный тензор второго ранга в трехмерном пространстве имеет всего 6 независимых компонент. Поэтому естественно вместо тензора , имеющего 3x3=9 компонент, ввести 6-и компонентную величину. Поступим следующим образом.

В технической механике принято записывать компоненты  в виде символи­чес­кого "вектора деформации" , имеющего 6 компонент:

(1.1.1.4)

Видим, что  - это просто столбец, состоящий из компонент . Первые три ком­поненты вектора представляют собой относительные изменения длин бесконечно малых отрезков, первоначально параллельных осям  координат . Последние три компоненты вектора являются деформациями сдвига, по величине равными изменениям углов между элементарными отрезками, первоначально параллельными осям координат, указанным в индексах.

В результате деформации упругого тела в нем возникают внутренние силы, стре­мящиеся вернуть тело в недеформированное состояние. Эти внутренние силы по своей природе являются поверхностными и называются внутренними напряжениями.

В теории упругости показывается, что напряжения могут быть математически описаны симметричным тензором второго ранга .

Как и тензор деформации , тензор напряжений  может быть представлен в виде симметричной матрицы (3x3):

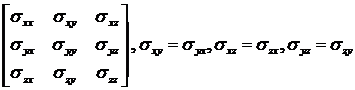
Поэтому вместо тензора напряжений  удобно ввести, по аналогии с "вектором деформаций" , 6-и компонентную величину, состоящую из независимых компонент тензора напряжений.

В технической механике принято вводить  символический  "вектор напряжений" , имеющий 6 компонент:

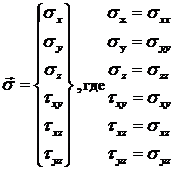              (1.1.1.5)

 

Первые три компоненты вектора  являются нормальными напряжениями (на площадках, перпендикулярных к осям координат ), а последние три компоненты - ка­са­тельными напряжениями.

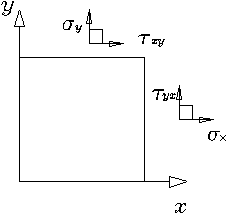
На рис. 1.1.2 демонстрируется направление компонент вектора .

Рис. 1.1.2

 

 

 

Закон Гука

 

Как известно, при достаточно малых деформациях твердого тела справедлив  закон Гука. Для задачи растяжения стержня он утверждает линейную связь между внешней силой  и возникающим перемещением .

В теории упругости принят обобщенный закон Гука, устанавливающий линейную зависимость компонент тензора (внутренних) напряжений  от компонент тензора деформа­ции .

Для однородной изотропной среды эта зависимость однозначно определяется сле­дующими упругими параметрами:

 - модуль упругости;

 - коэффициент Пуассона (0<  <1/2);

Введем также: 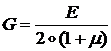  - модуль сдвига.

 

Указанная зависимость  от  в терминах компонент  векторов дается сле­дующими формулами:

 

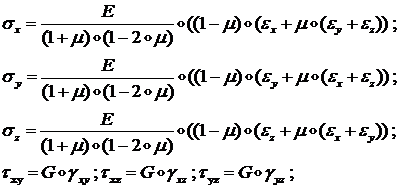
(1.1.1.6)

В матричной форме уравнения (1.1.1.6) имеют вид:

                               (1.1.1.7)

Здесь:  - матрица упругости;

 

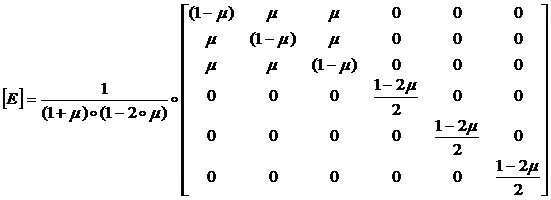 (1.1.1.8)

 

 

Энергия деформации упругого тела

 

Для вывода формулы энергии деформации упругого тела  заметим, что в соот­ветствии с законом сохранения энергии работа внешних сил  равна приращению энергии деформации  (диссипацией энергии пренебрегаем) :

Пусть работу по деформированию тела совершают объемные силы . Как известно из механики, работа  силы  на перемещении  равна: . В элементарном объеме  действует сила .

Поэтому элементарная работа объемных сил на перемещении равна:

 

а для всего объема тела: , где интегрирование ведется по всему объему тела.

В теории упругости показывается, что уравнение  равновесия сплошной упругой среды имеет вид:

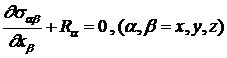
Поэтому выражение для элементарной работы  примет вид:

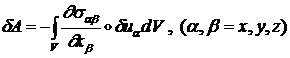
Здесь и дальше принято суммирование по паре одинаковых индексов. Нетрудно ви­деть, что в сумме, стоящей под знаком интеграла, всего 3x3=9 слагаемых.

Преобразуем подынтегральное выражение:

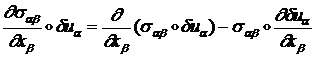
По теории Гаусса интеграл по объему тела 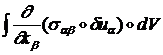 равен  интегралу по поверхности тела:

 

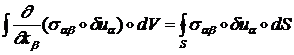
Рассматривая неограниченную среду, не деформированную на бесконечности, устремим границы тела в бесконечность; тогда можно считать, что на поверхности тела напряжения:

Поэтому формула для примет вид:

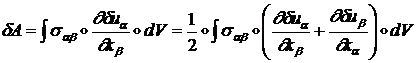
Последнее равенство справедливо вследствие симметрии тензора напряжений . Индекс объема  опущен.

Учитывая формулу (1.1.1.3) для тензора деформации и линейность операции диф­ференцирования, последнюю формулу запишем в виде:

Так как , то имеем для энергии деформации  [8]:

Полученная формула справедлива для деформации произвольной сплошной упру­гой среды и является, поэтому самой общей.

Получим теперь формулу для энергии деформации упругой среды, подчиняющейся закону Гука. В последнем случае компоненты  зависят линейно от компонент .

Тогда после интегрирования от нулевых деформаций  до  конечных деформаций  с учетом равенства:

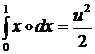
получим формулу для энергии произвольно деформированного тела, подчиняюще­го­ся закону Гука:

С учетом симметрии тензоров   и    сумма  равна:

Используя формулы (1.1.1.4) и (1.1.1.5) для связи компонент  с компонентами , а также компонент  с компонентами , последнее равенство перепишем в виде:

Если ввести транспонированный вектор - строку , то для энергии деформации получим формулу:

                 (1.1.1.9)

Для однородной упругой изотропной среды справедлива формула (1.1.1.7), связывающая :

где: - матрица упругости однородного изотропного тела, определяемая формулой (1.1.1.8)

В результате из формул (1.1.1.7) и (1.1.1.9) следует окончательная общеупотре­би­тельная формула для энергии деформации однородной упругой изотропной среды, подчи­няющейся закону Гука:

          (1.1.1.10)

Последняя формула является очень важной и на нее следует обратить особое вни­мание.

 

 

Граничные условия

 

Полученные в этом пункте формулы справедливы в любой точке упругого тела как сплошной среды. На границе (поверхности) тела справедливы дополнительные, так назы­ваемые граничные условия. Граничные условия получим на основе равенства, на границе тела силы , связанной с внутренними напряжениями- вектор нормали к поверхности), приложенной к телу внешней поверхностной силе :

    (1.1.1.11)

В случае если поверхность тела свободна от действия внешних сил, формула (1.1.1.11) принимает вид:

      (1.1.1.12)

 

Вариационный принцип Лагранжа

 

Уравнения равновесия упругого тела под воздействием внешних сил могут быть определены в механике с помощью вариационного принципа Лагранжа. Этот принцип утверждает, что уравнения равновесия получаются из функционала:

                             (1.1.1.13)

где:  - энергия деформации тела, определяемая формулой (1.1.1.10);

 - энергия работы внешних сил.

В случае если действуют объемные силы  и поверхностные силы , эта работа равна:

  (1.1.1.14)

Итак, функционал:  - зависит от поля вектора перемещения

Пусть  - вариация (приращение) . Тогда функционал  получает приращение:

 

Определение

 

Часть приращения функционала , линейная по вариации , называется первой вариацией функционала  и обозначается .

Принцип Лагранжа утверждает, что на истинном поле  перемещений  первая вариация равна нулю:

                                  (1.1.1.15)

В качестве примера рассмотрим функционал  вида:

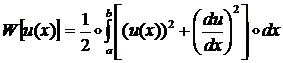                                                       (1.1.1.16)

где функция зависит от единственной переменной , заданной на отрезке .s

Пусть функция получает приращение .

Тогда приращение функционала   равно:

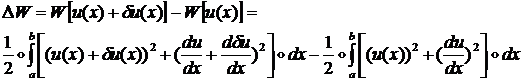
После возведения в квадрат сумм:

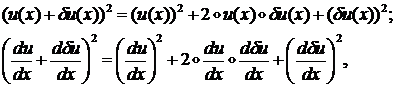
и сокращения одинаковых членов формула для  примет вид:

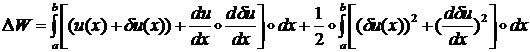
Первый интеграл в этой формуле линейно зависит от приращения . Поэтому, согласно определению, первая вариация функционала равна:

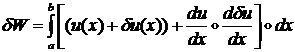
Принцип Лагранжа утверждает, что для "истинной" функции  первая вариация функционала равна нулю для всех допустимых вариаций "истинной" функции, т.е. для любой функции   справедливо равенство:

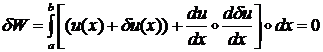
Покажем существование такой функции:

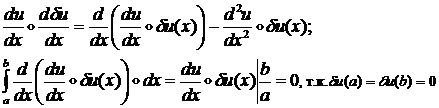
Поэтому получим уравнение:

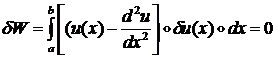
- для любой вариации . Последнее может быть справедливо только при условии:

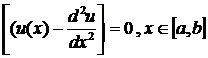       (1.1.1.17)

Итак, мы получили для искомой функции   дифференциальное уравнение второго порядка, называемое в вариационном исчислении уравнением Лагранжа. Зная значения  на концах отрезка , с помощью этого уравнения можно однозначно определить .

Действительно, общее решение полученного уравнения имеет вид:

где:  - произвольные константы.

Пусть: .

Тогда для определения  получим следующую систему алгебраических уравнений:

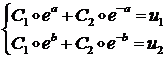
Решая ее, найдем:

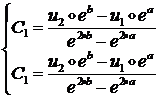
Рассмотренный здесь пример позволил нам проиллюстрировать идеи вариа­цион­ного исчисления: конкретизировать понятие приращения функционала , первой вариа­ции функционала , уравнение Лагранжа и др.

В дальнейшем мы будем использовать вариационный принцип Лагранжа для сис­тем с конечным числом степеней свободы, которые и рассматриваются в МКЭ.

Там, как мы увидим, уравнения  Лагранжа  принимают  достаточно простой вид.

Уравнения (1.1.1.10) - (1.1.1.15) определяют уравнения равновесия упругого тела для деформаций, определяемых законом Гука.

Изложенные результаты теории упругости в дальнейшем будут широко исполь­зо­ваться для развития применения МКЭ в механике.