Определение
собственных форм и частот
в системе ИСПА на процессорах
Intel I7 – 3930 и Intel I7 – 6910.
Александр
Александрович Мухин
В новой версии ИСПА решение нелинейных задач проводится с
использованием нового разреженного решателя (sparse direct solver). Решение любой
нелинейной задачи в МКЭ сводится к последовательному решению линейных задач.
При этом на каждом шаге изменяется или матрица (жесткости, больших перемещений
и т.д.) или правая часть или и матрица и правая часть одновременно. При определении
собственных форм и частот изменяется только правая часть. Факторизация матрицы
жесткости проводится один раз и дальше обрабатывается только измененная правая
часть. Можно, конечно, на каждом шаге запускать итерационный решатель, но это
существенно медленнее.
В данной статье рассмотрим решение задачи на собственные
колебания механической системы.
Запишем глобальные
"уравнения движения" механической системы:
(1.)
где:
- глобальная
матрица масс;
- глобальная
матрица жесткости;
- глобальные
вектора сил и степеней свободы,
Матрицы 
и 
являются
симметричными и положительно определенными.
Уравнения движения (1.) являются основными..
Собственные колебания механической системы совершаются
при отсутствии внешних сил. Полагая в "уравнениях движения" (1.)
правую часть 
равной нулю,
получим уравнения собственных колебаний:
(2)
Решение уравнений (2.) можно искать в виде гармоник с
частотой колебания 
:
(3)
Так как справедливы равенства:
то после подстановки 
или 
в уравнения (2.)
получим:
(4)
В уравнении (4) члены, зависящие от времени, опущены.
Система уравнений (4) имеет фундаментальное значение в теории колебаний. Ее решение
позволяет найти собственные частоты 
и собственные
формы колебаний 
механической системы, 
, где: 
- число степеней
свободы.
Общее решение системы уравнений (2.) имеет вид:
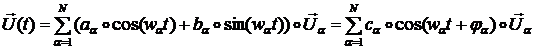(5)
Заметим, что в силу положительной определенности матриц и из (4.) следует:
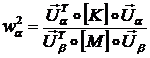(6)
т.е. собственные частоты 
, () являются действительными (положительными) числами, как
и должно быть для консервативной системы. За
исключением особых случаев,
Таким образом, задача нахождения собственных колебаний
механической системы свелась к задаче определения собственных частот и собственных
форм для системы алгебраических уравнений (4):
(7)
Как правило, в инженерной практике требуется найти низшие
частоты, поэтому в системе ИСПА
реализованы следующие методы определения собственных частот и собственных форм:
1) Метод обратных итераций подпространства;
2) Алгоритм Ланцоша;
3) Модифицированный алгоритм Ланцоша;
Во всех этих методах один раз проводится полная численная
факторизация матрицы жесткости и далее на каждой итерации проводится работа с N правых
частей. Это обеспечивает высокую скорость работы этих алгоритмов. Но не только
это. В новой версии ИСПА все векторные и матричные операции при определении
собственных форм и частот в системе ИСПА проводятся с
использованием расширения системы команд х86 для микропроцессоров Intel и AMD и также
оптимально используется OpenMP.
Решение будем проводить на компьютере с процессором Intel I7 – 3930, расширение системы команд для данного
процессора стандарт AVX (Advanced Vector Extensions). И на компьютере с процессором Intel I7 – 6900 расширение системы команд для данного
процессора стандарт AVX2 (Advanced Vector Extensions 2).
На рис. 1 представлена модель незакрепленного кубика,
каждая сторона которого разбита на 40 конечных элементов (8-ми узловые объемные
конечные элементы). Модель содержит 68 921 узлов и 64 000 элементов (206 763 уравнений). Количество
закрепленных степеней свободы – 0.
Рис 1.
Будем определять 50 первых собственных частот. Так как
кубик не закреплен , то первые шесть собственных
частот равны нулю. Время работы алгоритмов представлены в таблице 1.
Таблица 1.
|
|
Intel I7 – 3930 |
Intel I7 – 6900 |
|
Время полной численной факторизации матрицы жесткости |
12 сек |
6.1 сек |
|
Метод обратных итераций подпространства |
1 мин 44 сек |
45 сек |
|
Алгоритм Ланцоша |
2 мин 26 сек |
57 сек |
|
Модифицированный алгоритм Ланцоша |
35 сек |
15 сек |
Первая упругая форма и 50-ая форма собственных колебаний
кубика представлены на рис 1а и 1б соответственно.
Рис 1а.
Рис 1б.
500 первых собственных частот.
|
|
Intel I7 – 3930 |
Intel I7 – 6900 |
|
Время полной численной факторизации матрицы жесткости |
12 сек |
6.1 сек |
|
Модифицированный алгоритм Ланцоша |
3 мин 10 сек |
1 мин 42 сек |
500-ая форма собственных колебаний кубика представлены на рис 1в.
Рис 1в.
Данный пример интересен тем, что любой желающий, легко
сможет сделать такой же кубик в другом комплексе и сравнить скорость работы. И
еще один интересный момент. В случае незакрепленной конструкции решить линейные
уравнения итерационным методом не получится. В данном случае эффективно
работают только прямые методы.
На рис. 2 представлена модель колеса. Модель автоматически
сгенерирована с использованием 4-х узловых тетраэдров. Содержит 362 169 узлов и 1 438 639 элементов (1 084 470 уравнений). Количество
закрепленных степеней свободы – 2 037.
Рис 2.
Будем определять 50 первых собственных частот. Время работы
алгоритмов представлены в таблице 2.
Таблица 2.
|
|
Intel I7 – 3930 |
Intel I7 – 6900 |
|
Время полной численной факторизации матрицы жесткости |
6 сек |
2.3 сек |
|
Метод обратных итераций подпространства |
2 мин 41 сек |
1 мин 19 сек |
|
Алгоритм Ланцоша |
2 мин 32 сек |
1 мин 11 сек |
|
Модифицированный алгоритм Ланцоша |
1 мин 19 сек |
28 сек |
50-ая форма собственных колебаний колеса представлены на
рис 2а.
Рис 2а.
На рис 3 представлена конечно-элементная
модель мостового перегружателя. Модель автоматически сгенерирована с
использованием 4-х узловых тонких оболочек. Время автоматической генерации
такой модели составляет 8 сек.
Модель содержит
330 588 узлов и 340 090 элементов (1 812 558 уравнений).
Количество закрепленных степеней свободы – 12.
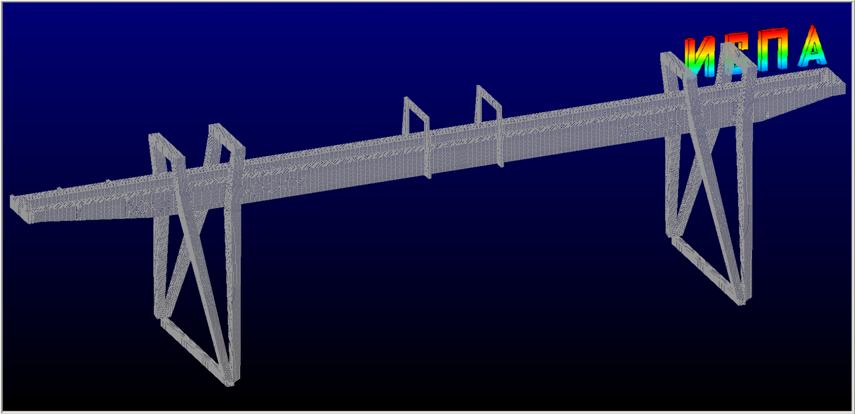
Рис 3.
Будем определять 50 первых собственных частот. Время
работы алгоритмов представлены в таблице 3.
Таблица 3.
|
|
Intel I7 – 3930 |
Intel I7 – 6900 |
|
Время полной численной факторизации матрицы жесткости |
4.7 сек |
1.7 сек |
|
Метод обратных итераций подпространства |
10 мин 26 сек |
5 мин 11 сек |
|
Алгоритм Ланцоша |
2 мин 51 сек |
1 мин 27 сек |
|
Модифицированный алгоритм Ланцоша |
1 мин 56 сек |
42 сек |
47-ая форма собственных колебаний мостового перегружателя представлены на рис 3а.
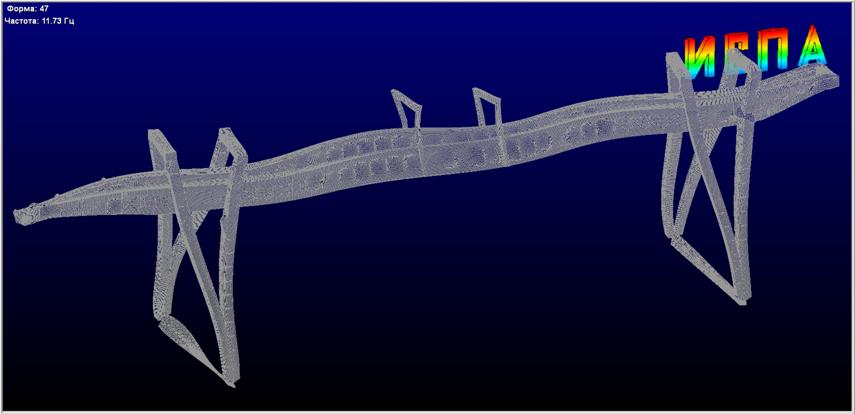
Рис 3а.
Проанализировав полученные результаты можно сделать
вывод, что использование расширенной системы команд AVX2 (Advanced Vector Extensions 2) в два раза ускоряет работу системы ИСПА при
определении собственных форм и частот.
В настоящий момент разрабатывается версия системы ИСПА с использование
расширенной системы команд AVX512.
Любой желающий может взять систему ИСПА в бесплатную
опытно-промышленную эксплуатацию и проверить скорость и точность работы ИСПА на
своем компьютере. Размерность решаемых задач в ИСПА, на момент написания данной
статьи, составляет до 70 000 000 узлов, 70 000 000 элементов,
200 000 000 степеней свободы (уравнений). Система ИСПА при решении
больших задач использует все физические и логические ядра процессора.
Ноябрь