в системе ИСПА.
Часть
2
Александр
Александрович Мухин
В данной статье речь пойдет о решении геометрически
нелинейных задач в системе ИСПА.
При решении линейных статических задач предполагается,
что и перемещения и деформации конструкции малы. Практически это означает, что
форма конечных элементов в процессе нагружения не
изменяется и что для деформаций можно использовать приближенные линейные
соотношения.
На практике эти предположения часто приводят к
неправильным результатам даже при малых деформациях, не превышающих предел
упругости материала конструкции. При точном определении перемещений ряда
конструкций может оказаться необходимым учет геометрической нелинейности.
Например, мембранные напряжения, которыми обычно пренебрегают при изгибе
пластин, могут оказаться причиной значительного уменьшения перемещений даже при
малых деформациях. С другой стороны, может оказаться, что нагрузка, при которой
прогиб увеличивается, достигается быстрее, чем это предсказывается линейной
теорией, и может возникнуть ситуация, в которой при продолжающемся
деформировании несущая способность будет падать. Это не что иное, как
классическая задача устойчивости конструкций. Такие задачи встречаются довольно
часто. Значение их особенно велико при расчете тонкостенных конструкций.
В геометрически нелинейной задаче деформации нелинейно зависят
от перемещений.
Независимо от того велики или малы перемещения (или
деформации), внутренние и внешние силы должны удовлетворять условиям равновесия.
Если перемещения определяются конечным
числом (узловых) параметров 
, то должно выполняться равенство
(1)
где:
- сумма внешних и
внутренних обобщенных сил, а матрица 
определяется из
соотношения
(2)
Черта означает, что при больших перемещениях деформации
нелинейно зависят от перемещений и матрица зависит от . Матрицу удобно представить
в виде
(3)
где:
- матрица определяющая бесконечно малые деформации,
- зависит от перемещений.
В “Теоретических основах ИСПА” показано, что в общем
случае является линейной
функцией перемещений.
Если деформации не очень велики, то можно использовать
обычное соотношение теории упругости
(4)
где:
- матрица упругих постоянных.
Однако в равной степени можно было бы использовать и любое нелинейное соотношение между
напряжениями и деформациями, поскольку задача сводится к решению нелинейной
системы уравнений (1).
Интегрирование в уравнении (1) производится по отдельным
элементам, а их вклады в уравнения равновесия в узлах суммируются обычным образом.
Ясно, что уравнение (1) следует решать
методом итераций и возможность применения общих методов очевидна.
Итерации метода Ньютона строятся следующим образом:
а) в качестве
первого приближения строится решение
по линейной теории упругости;
б) с помощью соотношения (1) определяется 
для заданной матрицы
и напряжений, определяемых равенством (4) или
любым другим линейным или нелинейным законом;
в) строится полная матрица тангенциальных жесткостей 
(подробное
описание построения матрицы тангенциальных жесткостей можно найти в
“Теоретических основах ИСПА”;
г) строится поправка
(5)
Процесс продолжается до тех пор, пока величина 
не
станет достаточно малой.
Все решение можно находить за один шаг для полной
действующей нагрузки. Однако, как и во всех нелинейных задачах, возникает возможность
неединственности решения и при этом может быть
найдено решение, не имеющее физического
смысла. В таких случаях целесообразно задавать нагрузку отдельными приращениями
и получать нелинейное решение для каждого приращения.
В новой версии ИСПА решение геометрически нелинейных
задач проводится с использованием нового
разреженного решателя (sparse direct solver). Решение геометрически нелинейной задачи
сводится к последовательному решению линейных задач. При этом на каждом шаге
создается новая матрица тангенциальных жесткостей и изменяется правая часть.
Решение будем проводить на компьютере с процессором Intel I7 – 3930, 64 Гб оперативной памяти. Операционная система WINDOWS 7 (64 разряда).
На рис. 1 представлена модель колеса. Модель
автоматически сгенерирована с использованием 4-х узловых тетраэдров. Содержит 362 169 узлов и 1 438 639 элементов (1 084 470 уравнений). Количество
закрепленных степеней свободы – 2 037.
Рис 1.
Время решения линейной статической задачи 42 сек. Время
полной численной факторизации матрицы жесткости составляет
5.7 сек.
На рис 1а представлены суммарные перемещения колеса. Максимальные
перемещения
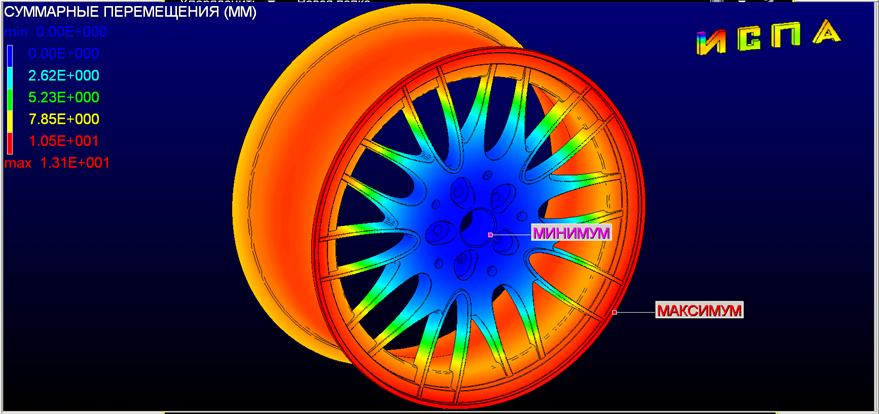
Рис 1а.
Теперь проведем геометрически нелинейный
расчет. После 6 итераций суммарные перемещения равны
Рис 1б.
На рис 2 представлена конечно-элементная модель мостового
перегружателя. Модель автоматически сгенерирована с использованием 4-х узловых
тонких оболочек. Время автоматической генерации такой модели составляет 14 сек.
Модель содержит
330 588 узлов и 340 090 элементов (1 812 558 уравнений).
Количество закрепленных степеней свободы – 12.
Рис 2.
Время решения линейной статической задачи 28 сек. Время
полной численной факторизации матрицы жесткости составляет
4.7 сек.
На рис 2а представлены суммарные перемещения.
Максимальные перемещения
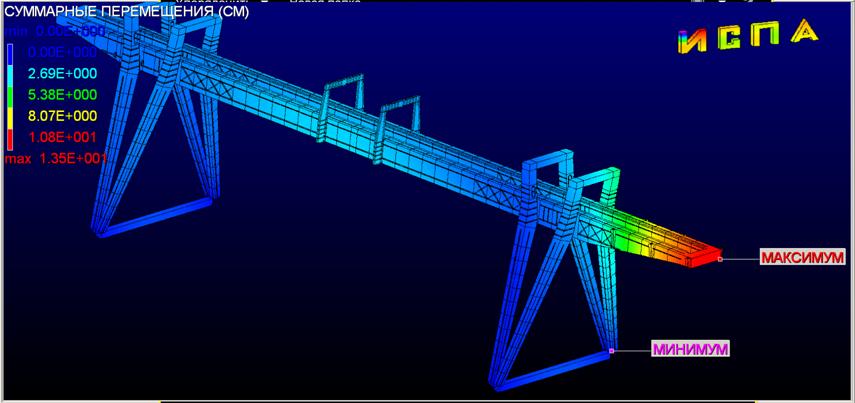
Рис 2а.
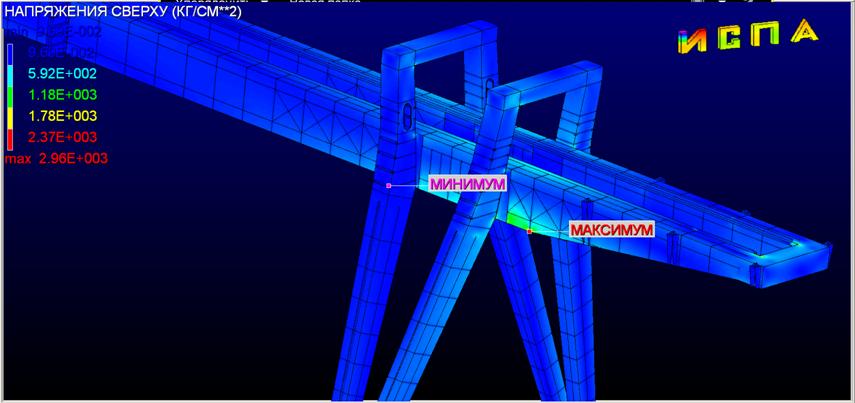
Рис 2б.
Теперь проведем геометрически нелинейный
расчет. После 5 итераций суммарные перемещения равны 13.5 см (рис 2в). Максимальные
эквивалентные напряжения 3010 кГ/см2 (рис 2г).
Время проведения 5
итераций составляет 3 мин 17 сек. Если дальше
продолжать итерации, то перемещения и напряжения не изменятся.
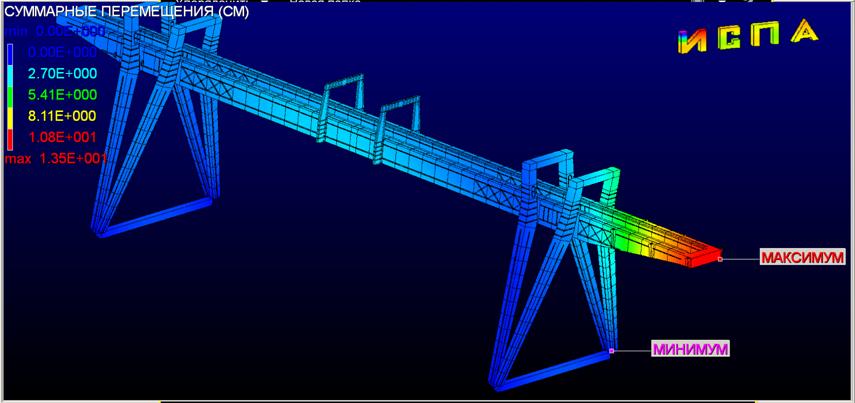
Рис 2в.
Рис 2г.
Геометрически нелинейные задачи встречаются довольно
часто. Значение их особенно актуально в авиационной и космической технике и при
конструировании других тонкостенных конструкций.
Любой желающий может взять систему ИСПА в бесплатную
опытно-промышленную эксплуатацию и проверить скорость и точность работы ИСПА на
своем компьютере. Размерность решаемых задач в ИСПА, на момент написания данной
статьи, составляет до 10 000 000 узлов, 10 000 000 элементов,
50 000 000 степеней свободы (уравнений). Система ИСПА при решении
больших задач использует до 48 физических ядер процессора при решении задач под
WINDOWS.
Апрель