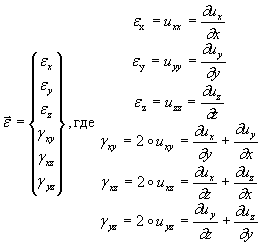Что такое конечный элемент
В методе конечных элементов, как это следует из названия, основополагающим
понятием является понятие конечного элемента. Пользователь должен знать какие
свойства заложены в конечные элементы, чтобы из них собрать математическую
модель. К сожалению, давая определение конечного элемента нельзя обойтись
фразами и предложениями общего характера, поэтому в этой статье будут
использованы формулы, требующие от читателя определенной математической
культуры. Итак, попробуем определить что же такое конечный элемент.
Рассмотрим тело, нагруженное произвольным образом. В результате действия
приложенных сил тело как-то деформируется и эта деформация может быть описана с
помощью поля перемещений: 
. Найти равновесное поле перемещений 
- вот задача теории упругости. Метод конечных элементов
позволяет приближенно найти поле перемещений упругого тела. Основная идея
метода конечных элементов состоит в том, что тело разбивается на совокупность
достаточно малых подобластей, называемых в дальнейшем конечными элементами. Эта
процедура называется дискретизацией тела. В пределах каждого конечного элемента
поле перемещений аппроксимируется с помощью функций формы по известным
значениям перемещений в узлах элемента 
(
- число узлов конечного элемента).
Заметим, что такой подход справедлив не только для метода конечных
элементов в механике, но и для других областей применения метода конечных
элементов, например, для задач теплопроводности, где вместо поля перемещений в
качестве основной неизвестной величины служит поле температур: 
.
С помощью функций формы аппроксимируются как поля неизвестных величин,
так и геометрия конечного элемента. В общем случае функции формы, употребляемые
для аппроксимации геометрии, отличаются от функций форм, использующихся для
аппроксимации полей неизвестных величин. Если эти функции формы совпадают, то
элемент называют изопараметрическим.
ОПРЕДЕЛЕНИЕ
Конечным элементом будем называть некоторую малую область тела в совокупности
с заданными в ней функциями формы, аппроксимирующими геометрию конечного
элемента и неизвестные величины.
Рассмотрим для общности трехмерную модель тела. Пусть мы провели
дискретизацию тела на трехмерные конечные элементы. В пределах каждого
конечного элемента, искомое поле перемещений 
:
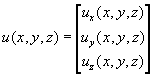
аппроксимируется по своим значениям 
в узлах элемента с помощью функций формы элемента 
:
(1)
Тогда вектор деформации 
, определяемый через перемещения, будет иметь следующую
аппроксимацию:
(2)
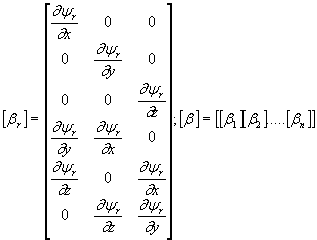
Здесь: 
- вектор степеней свободы элемента (
компонент);
- матрица деформирования элемента.
Итак, согласно (2), вектор деформации аппроксимируется в пределах конечного
элемента с помощью матрицы деформирования 
и вектора степеней свободы элемента 
.
Как мы знаем, энергия деформации упругого тела 
определяется формулой :
(3)
где: 
- 6-и компонентный вектор деформации ;
|
|
- матрица упругости однородной среды.
Интегрирование
ведется по объему тела.
Тогда в силу аддитивности интеграла энергия деформации тела 
равна сумме энергий деформации элементов 
, на которые разбито тело:
(4)
С помощью (2)
получим для 
:
(5)
где: 
- матрица жесткости элемента.
Матрица жесткости элемента является важнейшим понятием в приложении
метода конечных элементов в механике.
Так как полученная здесь формула для матрицы жесткости является общей,
выпишем ее еще раз:
(6)
Матрица жесткости 
имеет размерность (
), где 
- число степеней свободы конечного элемента.
Матрица 
- есть матрица деформирования элемента.
Собственно говоря, конечный элемент можно считать построенным, если
построена его матрица жесткости.
Пусть: 
- силы, действующие в узлах конечного элемента.
Тогда работа этих сил на узловых перемещениях, в соответствии с определением
работы в механике, равна:
(7)
где: 
Как следует из принципа Лагранжа, конечный элемент будет характеризоваться
потенциалом 
:
(8)
С помощью (5) и (7)
получим:
(9)
Видим что 
- есть просто функция от 
, так что первая вариация 
будет просто равна дифференциалу
В соответствии с принципом Лагранжа первая вариация 
, а значит и дифференциал 
равны нулю.
Но равенство нулю дифференциала функции возможно тогда, когда равны
нулю все ее первые производные, т.е. уравнение Лагранжа для метода конечных
элементов в механике примет вид:
(10)
В результате мы получили уравнения равновесия конечного элемента,
представляющие собой систему линейных неоднородных алгебраических уравнений
относительно неизвестного вектора степеней свободы элемента 
:
(11)
Итак, мы нашли что узловые силы 
и узловые перемещения 
конечного элемента связаны между собой с помощью матрицы
жесткости элемента 
.
Этим и определяется особое значение матрицы жесткости конечного элемента.
Заметим, что из формулы (6), определяющей матрицу жесткости элемента,
следует ее симметричность:
(для любой пары индексов 
).
Кроме того, так как энергия деформации элемента 
всегда положительна и равна нулю только при отсутствии деформаций,
то из (5) следует, что матрица жесткости элемента 
положительно определенная.
Этими двумя свойствами исчерпываются основные свойства матрицы жесткости
элемента.
Подведем итоги. Мы дали определение конечного элемента и вывели формулу
для матрицы жесткости конечного элемента. У пользователя может возникнуть
закономерный вопрос. Зачем мне разбираться в этих формулах? Моя задача
создавать модели и проводить расчетные исследования. Ответ скрывается в
многообразии конечных элементов. Например, в системе ИСПА их более 40. И это
многообразие связано не только с формой элемента и типом напряженного
состояния, но и с функциями аппроксимирующими неизвестные величины.
Оказывается, что при одной и той же форме элементов (внешне не отличить),
расчетные данные отличаются в 30-40 раз. Именно этому будет посвящена следующая
статья.