Объемные конечные элементы для расчета тонкостенных конструкций.

Александр Мухин

То, что толстостенные и массивные конструкции можно рассчитывать объемными элементами является очевидным фактом. Само название объемные элементы говорит об их предназначении. Они и создавались для расчета массивных объемных конструкций. А вот можно ли объемными элементами моделировать тонкостенные конструкции? Постараюсь в этой статье ответить на этот вопрос.

Под словом тонкостенная конструкция будем понимать такую конструкцию, у которой один или два размера, как минимум, на порядок больше остальных размеров.

Тестировать будем следующие элементы:

- 4-х узловой тетраэдр. Самый простой по форме и, по сути, объемный элемент. Четыре узла в вершинах элемента позволяют задать линейный закон изменения неизвестных по элементу.

- 10-ти узловой тетраэдр. Четыре узла в вершинах элемента и шесть узлов на ребрах. Это уже квадратичный элемент.

- 20-ти узловой тетраэдр. Четыре узла в вершинах элемента и 12 узлов на ребрах и четыре узла в центре граней. Это уже кубичный элемент.

Эти элементы не случайно выбраны для тестирования. В системе ИСПА разработан автоматический генератор тетраэдральных сеток по геометрическим моделям.

Также протестируем:

- 8-ми узловой гексаэдр. Восемь узлов в вершинах элемента позволяют задать линейный закон изменения неизвестных по элементу.

- 20-ти узловой гексаэдр. Восемь узла в вершинах элемента и 12 узлов на ребрах. Это уже квадратичный элемент.

В качестве теста возьмем тонкую пластину размером 100х100 и толщиной 1. Толщина на два порядка меньше двух других размеров пластины. Модуль упругости , коэффициент Пуассона 0.3.. Жестко закрепим по краям и дадим нагрузку в виде постоянного давления по всей площади величиной . Зададим разбиение 10х10х1. Результаты в виде максимального перемещения представлены в таблице 1.

таблица 1. Разбиение 10х10.

Тип элемента	Перемещение
4-х узловой тетраэдр	0.069
10-ти узловой тетраэдр	5.22
20-ти узловой тетраэдр	6.87
20-ти узловой гексаэдр	6.42
8-ми узловой гексаэдр	0.25
8-ми узловая пластина	6.89

Теперь зададим разбиение 20х20х1. Результаты в виде максимального перемещения представлены в таблице 2.

таблица 2. Разбиение 20х20.

Тип элемента	Перемещение
4-х узловой тетраэдр	0.24
10-ти узловой тетраэдр	6.66
20-ти узловой тетраэдр	6.94
20-ти узловой гексаэдр	6.73
8-ми узловой гексаэдр	0.88
8-ми узловая пластина	6.91

Проанализировав результаты расчетов, приходим к выводу, что 4-х узловой тетраэдр и 8-ми узловой гексаэдр, дают заниженный результат по перемещениям при данном разбиении пластины. Это связано с линейным законом аппроксимации неизвестных в этих элементах. Элементы с промежуточными узлами, дают хорошие результаты.

Увеличим до 100 количество чисел деления на ребрах пластины. Моделировать будем 4-х узловым тетраэдром и 8-ми узловым гексаэдром. Результаты представлены в таблице 3.

таблица 3. Разбиение 100х100.

Тип элемента	Перемещение
4-х узловой тетраэдр	0.41
8-ми узловой гексаэдр	0.46

Даже при таком разбиении пластины результаты далеки до точного. Исходя из полученных результатов, делаем вывод, что эти элементы могут привести к большой ошибке при расчете тонкостенных конструкций.

Практический опыт показывает, что если по толщине задать разбиение 4-5 элементов, то в этом случае можно применять 4-х узловые тетраэдры (рис 1).

Рис 1. Конечно-элементная модель из 4-х узловых тетраэдров.

Но для тонкостенных конструкций для этого потребуется очень большое количество элементов, поэтому нужно применять 10-ти и 20-ти узловые тетраэдры. Пример сборки автоматически сгенерированной из 20-ти узловых тетраэдров показан на рисунках 2 и 3. Очень удобно для расчетов брать модели сборочных конструкций и автоматически набирать тераэдральные элементы. Тем более, как было показано выше, точность 20-ти узловых тетраэдров лучше, чем 20-ти узловых гексаэдров. На сегодняшний день 20-ти узловой тетраэдр – самый точный объемный конечный элемент в системе ИСПА.

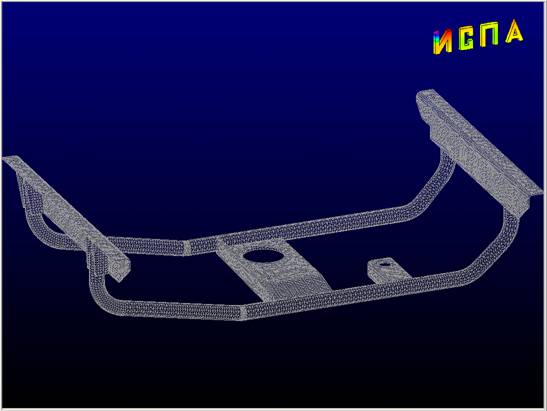
Рис 2. Конечно-элементная модель кронштейна из 20-ти узловых тетраэдров.

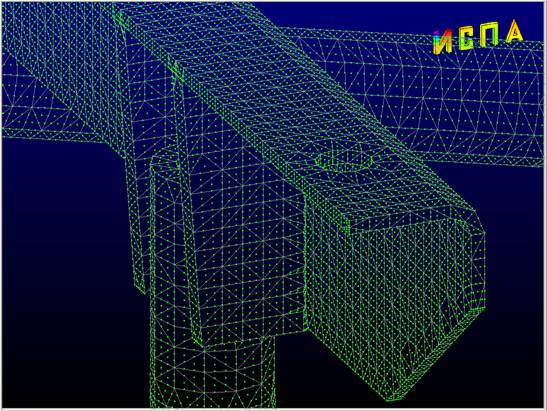
Рис 3. Фрагмент конечно-элементная модель кронштейна из 20-ти узловых тетраэдров.

Расчетная практика показывает, что для аппроксимации геометрии реальных конструкций требуется большое количество элементов. Допустимое соотношение сторон должно быть меньше 10. Матрица жесткости в этом случае получается большой размерности и с большой связанностью по ширине ленты. Можно, конечно, такие матрицы решать прямыми методами с оптимизацией по ширине ленты или с оптимизацией на заполняемость при решении, но на это уйдет много времени. Поэтому, в системе ИСПА для решения конечно-элементных сеток из 10-ти и 20-ти тетраэдров реализована возможность расчетов итерационным методом с использованием видео ускорителей.

Рис 4. Конечно-элементная модель кольца из 10-ти узловых тетраэдров.

Рис 5. Фрагмент конечно-элементная модель кольца из 10-ти узловых тетраэдров.

На момент написания данной статьи автор рекомендует использовать видео ускорители фирмы NVIDIA TESLA C 2070 (2050) или TESLA S 2070 (2050). Для примера приведу конечно-элементную модель из 20-ти узловых тетраэдров рисунок 4 и 5. В модели 178 653 элементов, 354 868 узлов, 1 057 182 степеней свободы. Время решения уравнений с использованием видео ускорителя составляет 7 минут.

Июнь 2010 г.